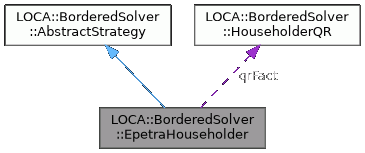
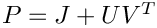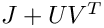Bordered system solver strategy based on Householder transformations. More...
#include <LOCA_BorderedSolver_EpetraHouseholder.H>
Public Member Functions | |
| EpetraHouseholder (const Teuchos::RCP< LOCA::GlobalData > &global_data, const Teuchos::RCP< LOCA::Parameter::SublistParser > &topParams, const Teuchos::RCP< Teuchos::ParameterList > &solverParams) | |
| Constructor. | |
| virtual | ~EpetraHouseholder () |
| Destructor. | |
| virtual void | setMatrixBlocks (const Teuchos::RCP< const LOCA::BorderedSolver::AbstractOperator > &op, const Teuchos::RCP< const NOX::Abstract::MultiVector > &blockA, const Teuchos::RCP< const LOCA::MultiContinuation::ConstraintInterface > &blockB, const Teuchos::RCP< const NOX::Abstract::MultiVector::DenseMatrix > &blockC) |
| Set blocks. | |
| virtual NOX::Abstract::Group::ReturnType | initForSolve () |
| Intialize solver for a solve. | |
| virtual NOX::Abstract::Group::ReturnType | initForTransposeSolve () |
| Intialize solver for a transpose solve. | |
| virtual NOX::Abstract::Group::ReturnType | apply (const NOX::Abstract::MultiVector &X, const NOX::Abstract::MultiVector::DenseMatrix &Y, NOX::Abstract::MultiVector &U, NOX::Abstract::MultiVector::DenseMatrix &V) const |
| Computed extended matrix-multivector product. | |
| virtual NOX::Abstract::Group::ReturnType | applyTranspose (const NOX::Abstract::MultiVector &X, const NOX::Abstract::MultiVector::DenseMatrix &Y, NOX::Abstract::MultiVector &U, NOX::Abstract::MultiVector::DenseMatrix &V) const |
| Computed extended matrix transpose-multivector product. | |
| virtual NOX::Abstract::Group::ReturnType | applyInverse (Teuchos::ParameterList ¶ms, const NOX::Abstract::MultiVector *F, const NOX::Abstract::MultiVector::DenseMatrix *G, NOX::Abstract::MultiVector &X, NOX::Abstract::MultiVector::DenseMatrix &Y) const |
| Solves the extended system using the technique described above. | |
| virtual NOX::Abstract::Group::ReturnType | applyInverseTranspose (Teuchos::ParameterList ¶ms, const NOX::Abstract::MultiVector *F, const NOX::Abstract::MultiVector::DenseMatrix *G, NOX::Abstract::MultiVector &X, NOX::Abstract::MultiVector::DenseMatrix &Y) const |
| Solves the transpose of the extended system as defined above. | |
 Public Member Functions inherited from LOCA::BorderedSolver::AbstractStrategy Public Member Functions inherited from LOCA::BorderedSolver::AbstractStrategy | |
| AbstractStrategy () | |
| Constructor. | |
| virtual | ~AbstractStrategy () |
| Destructor. | |
| virtual void | setMatrixBlocksMultiVecConstraint (const Teuchos::RCP< const LOCA::BorderedSolver::AbstractOperator > &op, const Teuchos::RCP< const NOX::Abstract::MultiVector > &blockA, const Teuchos::RCP< const NOX::Abstract::MultiVector > &blockB, const Teuchos::RCP< const NOX::Abstract::MultiVector::DenseMatrix > &blockC) |
| Set blocks with multivector constraint. | |
Protected Types | |
| enum | PRECONDITIONER_METHOD { JACOBIAN , SMW } |
| Enumerated type indicating preconditioner method. | |
Protected Attributes | |
| Teuchos::RCP< LOCA::GlobalData > | globalData |
| Global data object. | |
| Teuchos::RCP< Teuchos::ParameterList > | solverParams |
| Solver parameters. | |
| Teuchos::RCP< LOCA::Epetra::Group > | grp |
| Pointer to group storing J. | |
| Teuchos::RCP< const LOCA::BorderedSolver::AbstractOperator > | op |
| Teuchos::RCP< const NOX::Abstract::MultiVector > | A |
| Pointer to A block. | |
| Teuchos::RCP< const NOX::Abstract::MultiVector > | B |
| Pointer to B block. | |
| Teuchos::RCP< const NOX::Abstract::MultiVector::DenseMatrix > | C |
| Pointer to C block. | |
| Teuchos::RCP< const LOCA::MultiContinuation::ConstraintInterfaceMVDX > | constraints |
| Pointer to constraint interface. | |
| LOCA::BorderedSolver::HouseholderQR | qrFact |
| QR Factorization object. | |
| Teuchos::RCP< NOX::Abstract::MultiVector > | house_x |
| Solution component of Householder multivec. | |
| NOX::Abstract::MultiVector::DenseMatrix | house_p |
| Parameter component of Householder multivec. | |
| NOX::Abstract::MultiVector::DenseMatrix | T |
| T matrix in compact WY representation. | |
| NOX::Abstract::MultiVector::DenseMatrix | R |
| R matrix in QR factorization. | |
| Teuchos::RCP< NOX::Abstract::MultiVector > | U |
| U matrix in low-rank update form P = J + U*V^T. | |
| Teuchos::RCP< NOX::Abstract::MultiVector > | V |
| V matrix in low-rank update form P = J + U*V^T. | |
| Teuchos::RCP< NOX::Abstract::MultiVector > | house_x_trans |
| Solution component of Householder multivec for transposed system. | |
| NOX::Abstract::MultiVector::DenseMatrix | house_p_trans |
| Parameter component of Householder multivec for transposed system. | |
| NOX::Abstract::MultiVector::DenseMatrix | T_trans |
| T matrix in compact WY representation for transposed system. | |
| NOX::Abstract::MultiVector::DenseMatrix | R_trans |
| R matrix in QR factorization for transposed system. | |
| Teuchos::RCP< NOX::Abstract::MultiVector > | U_trans |
| U matrix in low-rank update form P = J + U*V^T for transposed system. | |
| Teuchos::RCP< NOX::Abstract::MultiVector > | V_trans |
| V matrix in low-rank update form P = J + U*V^T for transposed system. | |
| Teuchos::RCP< const NOX::Abstract::MultiVector > | Ablock |
| Pointer to A block as an Epetra multivector. | |
| Teuchos::RCP< const NOX::Abstract::MultiVector > | Bblock |
| Pointer to B block as an Epetra multivector. | |
| Teuchos::RCP< NOX::Abstract::MultiVector > | Ascaled |
| Pointer to scaled A block. | |
| Teuchos::RCP< NOX::Abstract::MultiVector > | Bscaled |
| Pointer to scaled B block. | |
| Teuchos::RCP< NOX::Abstract::MultiVector::DenseMatrix > | Cscaled |
| Pointer to scaled C block. | |
| Teuchos::RCP< NOX::Epetra::LinearSystem > | linSys |
| Pointer to linear system. | |
| Teuchos::RCP< Epetra_Operator > | epetraOp |
| Pointer to Epetra operator. | |
| Teuchos::RCP< const Epetra_BlockMap > | baseMap |
| Pointer to base map for block vectors. | |
| Teuchos::RCP< const Epetra_BlockMap > | globalMap |
| Pointer to global map for block vectors. | |
| int | numConstraints |
| Number of constraint equations. | |
| bool | isZeroA |
| flag indicating whether A block is zero | |
| bool | isZeroB |
| flag indicating whether B block is zero | |
| bool | isZeroC |
| flag indicating whether C block is zero | |
| bool | isValidForSolve |
| Flag indicating whether constraint factorization for solve has been computed. | |
| bool | isValidForTransposeSolve |
| Flag indicating whether constraint factorization for transpoe solve has been computed. | |
| Teuchos::BLAS< int, double > | dblas |
| BLAS Wrappers. | |
| bool | scale_rows |
| Whether we should scale augmented rows to have unit 2-norm. | |
| std::vector< double > | scale_vals |
| Scale values for each row. | |
| PRECONDITIONER_METHOD | precMethod |
| Preconditioner method. | |
| bool | includeUV |
| Flag indicating whether to include U*V^T terms in preconditioner. | |
| bool | use_P_For_Prec |
| Flag indicating whether to use P = J + U*V^T in preconditioner. | |
| bool | isComplex |
| Flag indicating whether we are doing a complex solve. | |
| double | omega |
| Frequency for complex systems. | |
Detailed Description
Bordered system solver strategy based on Householder transformations.
This class solves the extended system of equations
![\[
\begin{bmatrix}
J & A \\
B^T & C
\end{bmatrix}
\begin{bmatrix}
X \\
Y
\end{bmatrix} =
\begin{bmatrix}
F \\
G
\end{bmatrix}
\]](form_314.png)
using Householder tranformations. The algorithm works as follows: First consider a slightly rearranged version of the extended system of equations:
![\[
\begin{bmatrix}
C & B^T \\
A & J
\end{bmatrix}
\begin{bmatrix}
Y \\
X
\end{bmatrix} =
\begin{bmatrix}
G \\
F
\end{bmatrix}.
\]](form_318.png)
Let
![\[
Q^T
\begin{bmatrix}
C^T \\
B
\end{bmatrix} =
\begin{bmatrix}
R \\
0
\end{bmatrix}
\]](form_319.png)
be the QR decomposition of the constraints matrix where 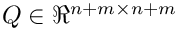
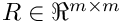
![\[
\begin{bmatrix}
Z_Y \\
Z_X
\end{bmatrix} = Q^T
\begin{bmatrix}
Y \\
X
\end{bmatrix},
\]](form_322.png)
then the extended system of equations is equivalent to
![\[
\begin{bmatrix}
R^T & 0 \\
[A & J] Q
\end{bmatrix}
\begin{bmatrix}
Z_Y \\
Z_X
\end{bmatrix} =
\begin{bmatrix}
G \\
F
\end{bmatrix}
\]](form_323.png)
and hence
![\[
\begin{split}
Z_Y &= R^{-T} G \\
[A \;\; J] Q
\begin{bmatrix}
0 \\
Z_X
\end{bmatrix} &= F - [A \;\; J] Q
\begin{bmatrix}
Z_Y \\
0
\end{bmatrix}.
\end{split}
\]](form_324.png)
This last equation equation can be written
![\[
P Z_X = \tilde{F}
\]](form_325.png)
where 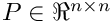
![\[
P Z_X = [A \;\; J] Q
\begin{bmatrix}
0 \\
Z_X
\end{bmatrix}
\]](form_327.png)
and
![\[
\tilde{F} = F - [A \;\; J] Q
\begin{bmatrix}
Z_Y \\
0
\end{bmatrix}.
\]](form_328.png)
We then recover 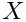
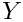
![\[
\begin{bmatrix}
Y \\
X
\end{bmatrix} = Q
\begin{bmatrix}
Z_Y \\
Z_X
\end{bmatrix}.
\]](form_331.png)
It can be further shown that the 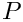
![\[
P = J + U V^T
\]](form_333.png)
where 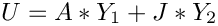
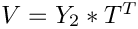
![$Y = [Y_1 ; Y_2]$](form_336.png)
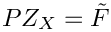
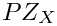
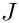
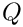
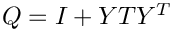
The operator representing 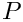
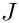
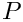
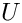
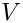
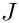
The class is intialized via the solverParams parameter list argument to the constructor. The parameters this class recognizes are:
-
"Preconditioner Method" – [string] (default: "Jacobian") - Method for preconditioning the
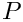
-
"Jacobian" (default) – Use the preconditioner for
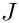
-
"SMW" – Use the Sherman-Morrison-Woodbury formula for the inverse of
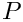
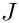
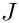
-
"Jacobian" (default) – Use the preconditioner for
- "Scale Augmented Rows" – [bool] (default: true) - Scale augmented rows to unit 2-norm before computing QR factorization.
-
"Include UV In Preconditioner" – [bool] (default: false) - Flag indicating whether to use the
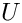
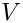
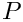
-
"Use P For Preconditioner" – [bool] (default: false) - Flag indicating whether to use the representation of
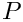
- "Transpose Solver Method" – [string] (default: "Transpose Preconditioner") Method for preconditioning the transpose linear system. See LOCA::Epetra::TransposeLinearSystem::Factory for available choices.
Constructor & Destructor Documentation
◆ EpetraHouseholder()
| LOCA::BorderedSolver::EpetraHouseholder::EpetraHouseholder | ( | const Teuchos::RCP< LOCA::GlobalData > & | global_data, |
| const Teuchos::RCP< LOCA::Parameter::SublistParser > & | topParams, | ||
| const Teuchos::RCP< Teuchos::ParameterList > & | solverParams | ||
| ) |
Constructor.
- Parameters
-
global_data [in] Global data object topParams [in] Parsed top-level parameter list solverParams [in] Bordered solver parameters as described above
References globalData, includeUV, precMethod, scale_rows, solverParams, and use_P_For_Prec.
Member Function Documentation
◆ apply()
|
virtual |
Computed extended matrix-multivector product.
Computes
![\[
\begin{bmatrix}
U \\
V
\end{bmatrix} =
\begin{bmatrix}
J & A \\
B^T & C
\end{bmatrix}
\begin{bmatrix}
X \\
Y
\end{bmatrix} =
\begin{bmatrix}
J*X + A*Y \\
B^T*X + C*Y
\end{bmatrix}.
\]](form_316.png)
Implements LOCA::BorderedSolver::AbstractStrategy.
References NOX::Abstract::Group::Failed, NOX::Abstract::MultiVector::multiply(), and NOX::Abstract::MultiVector::update().
◆ applyInverse()
|
virtual |
Solves the extended system using the technique described above.
The params argument is the linear solver parameters. If isZeroF or isZeroG is true, than the corresponding F or G pointers may be NULL.
Note that if either the A or B blocks are zero, the system is solved using a simple block elimination scheme instead of the Householder scheme.
Implements LOCA::BorderedSolver::AbstractStrategy.
References NOX::Abstract::MultiVector::init(), NOX::Abstract::Group::Ok, LOCA::BorderedSolver::LowerTriangularBlockElimination::solve(), and LOCA::BorderedSolver::UpperTriangularBlockElimination::solve().
◆ applyInverseTranspose()
|
virtual |
Solves the transpose of the extended system as defined above.
The params argument is the linear solver parameters.
Implements LOCA::BorderedSolver::AbstractStrategy.
References NOX::Abstract::MultiVector::init(), NOX::Abstract::Group::Ok, LOCA::BorderedSolver::LowerTriangularBlockElimination::solveTranspose(), and LOCA::BorderedSolver::UpperTriangularBlockElimination::solveTranspose().
◆ applyTranspose()
|
virtual |
Computed extended matrix transpose-multivector product.
Computes
![\[
\begin{bmatrix}
U \\
V
\end{bmatrix} =
\begin{bmatrix}
J^T & B \\
A^T & C
\end{bmatrix}
\begin{bmatrix}
X \\
Y
\end{bmatrix} =
\begin{bmatrix}
J^T*X + B*Y \\
A^T*X + C^T*Y
\end{bmatrix}.
\]](form_317.png)
Implements LOCA::BorderedSolver::AbstractStrategy.
References NOX::Abstract::Group::Failed, and NOX::Abstract::MultiVector::multiply().
◆ initForSolve()
|
virtual |
Intialize solver for a solve.
This should be called after setMatrixBlocks(), but before applyInverse().
Implements LOCA::BorderedSolver::AbstractStrategy.
References NOX::Abstract::Group::Ok, and NOX::ShapeCopy.
◆ initForTransposeSolve()
|
virtual |
Intialize solver for a transpose solve.
This should be called after setMatrixBlocks(), but before applyInverseTranspose().
Implements LOCA::BorderedSolver::AbstractStrategy.
References NOX::Abstract::Group::Ok, and NOX::ShapeCopy.
◆ setMatrixBlocks()
|
virtual |
Set blocks.
The blockA or blockC pointer may be null if either is zero. Whether block B is zero will be determined by querying blockB via ConstraintInterface::isConstraintDerivativesXZero.
Implements LOCA::BorderedSolver::AbstractStrategy.
The documentation for this class was generated from the following files:
- LOCA_BorderedSolver_EpetraHouseholder.H
- LOCA_BorderedSolver_EpetraHouseholder.C