Simple example subclass for Spmd tridiagonal matrices. More...

#include <ExampleTridiagSpmdLinearOp.hpp>

Inheritance diagram for ExampleTridiagSpmdLinearOp< Scalar >:

[legend]

Public Member Functions
	ExampleTridiagSpmdLinearOp ()

	ExampleTridiagSpmdLinearOp (const Teuchos::RCP< const Teuchos::Comm< Thyra::Ordinal > > &comm, const Thyra::Ordinal localDim, const Teuchos::ArrayView< const Scalar > &lower, const Teuchos::ArrayView< const Scalar > &diag, const Teuchos::ArrayView< const Scalar > &upper)

void	initialize (const Teuchos::RCP< const Teuchos::Comm< Thyra::Ordinal > > &comm, const Thyra::Ordinal localDim, const Teuchos::ArrayView< const Scalar > &lower, const Teuchos::ArrayView< const Scalar > &diag, const Teuchos::ArrayView< const Scalar > &upper)

Public Member Functions inherited from Thyra::LinearOpDefaultBase< Scalar >
std::string	description () const
	Default description that gives the label, type, and dimenstion .

void	describe (Teuchos::FancyOStream &out, const Teuchos::EVerbosityLevel verbLevel) const
	Generates a default outputting for all linear operators.

Public Member Functions inherited from Thyra::LinearOpBase< Scalar >
bool	opSupported (EOpTransp M_trans) const
	Return if the `M_trans` operation of `apply()` is supported or not.

void	apply (const EOpTransp M_trans, const MultiVectorBase< Scalar > &X, const Ptr< MultiVectorBase< Scalar > > &Y, const Scalar alpha, const Scalar beta) const
	Apply the linear operator to a multi-vector : `Y = alphaop(M)X + beta*Y`.

virtual RCP< const LinearOpBase< Scalar > >	clone () const
	Clone the linear operator object (if supported).

Protected Member Functions
Teuchos::RCP< const Thyra::VectorSpaceBase< Scalar > >	range () const

Teuchos::RCP< const Thyra::VectorSpaceBase< Scalar > >	domain () const

bool	opSupportedImpl (Thyra::EOpTransp M_trans) const

void	applyImpl (const Thyra::EOpTransp M_trans, const Thyra::MultiVectorBase< Scalar > &X_in, const Teuchos::Ptr< Thyra::MultiVectorBase< Scalar > > &Y_inout, const Scalar alpha, const Scalar beta) const

Protected Member Functions inherited from Thyra::LinearOpBase< Scalar >

Additional Inherited Members
Related Symbols inherited from Thyra::LinearOpBase< Scalar >
template<class Scalar >
bool	isFullyUninitialized (const LinearOpBase< Scalar > &M)
	Determines if a linear operator is in the "Fully Uninitialized" state or not.

template<class Scalar >
bool	isPartiallyInitialized (const LinearOpBase< Scalar > &M)
	Determines if a linear operator is in the "Partially Initialized" state or not.

template<class Scalar >
bool	isFullyInitialized (const LinearOpBase< Scalar > &M)
	Determines if a linear operator is in the "Fully Initialized" state or not.

template<class Scalar >
bool	opSupported (const LinearOpBase< Scalar > &M, EOpTransp M_trans)
	Determines if an operation is supported for a single scalar type.

template<class Scalar >
void	apply (const LinearOpBase< Scalar > &M, const EOpTransp M_trans, const MultiVectorBase< Scalar > &X, const Ptr< MultiVectorBase< Scalar > > &Y, const Scalar alpha=static_cast< Scalar >(1.0), const Scalar beta=static_cast< Scalar >(0.0))
	Non-member function call for `M.apply(...)`.

void	apply (const LinearOpBase< double > &M, const EOpTransp M_trans, const MultiVectorBase< double > &X, const Ptr< MultiVectorBase< double > > &Y, const double alpha=1.0, const double beta=0.0)
	Calls `apply<double>(...)`.

Detailed Description

template<class Scalar>
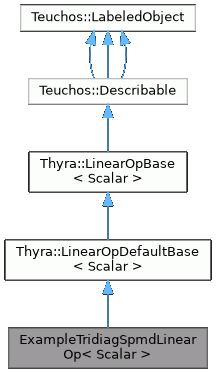
class ExampleTridiagSpmdLinearOp< Scalar >

Simple example subclass for Spmd tridiagonal matrices.

This subclass represents a linear operator for tridiagonal matrices of the global form:

$M= \left[\begin{array}{ccccc} d_{(1)} & u_{(1)} \\ l_{(1)} & d_{(2)} & u_{(2)} \\ & \ddots & \ddots & \ddots \\ & & l_{(n-2)} & d_{(n-1)} & u_{(n-1)} \\ & & & l_{(n-1)} & d_{(n)} \end{array}\right].$

If there is only 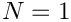processes then the arrays lower[], diag[], and upper[] of dimension localDim-1, localDim and localDim-1 respectively are stored (see initialize()).

If there 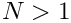processes then locally this class stores slightly different arrays of data depending on which process this is and process-to-process communication is required.

On process 0 with local vector elements the following sub-matrix is stored:

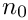
$\left[\begin{array}{cccccc} d_{(1)} & u_{(1)} \\ l_{(1)} & d_{(2)} & u_{(2)} \\ & \ddots & \ddots & \ddots \\ & & l_{(n_0-2)} & d_{(n_0-1)} & u_{(n_0-1)} \\ & & & l_{(n_0-1)} & d_{(n_0)} & u_{(n_0)} \end{array}\right].$

In this case, arrays lower[], diag[], and upper[] of dimension localDim-1, localDim and localDim respectively are stored (see initialize()).
On process , where , with local offset and local vector elements the following sub-matrix is stored:

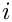
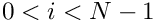
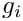
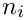
$\left[\begin{array}{cccccc} l_{(g_i)} & d_{(g_i+1)} & u_{(g_i+1)} \\ & \ddots & \ddots & \ddots \\ & & & l_{(g_i+n_i-1)} & d_{(g_i+n_i)} & u_{(g_i+n_i)} \end{array}\right].$

In this case, arrays lower[], diag[], and upper[] of dimension localDim, localDim and localDim respectively are stored (see initialize()).
On process with local offset $g_{N-1}$ and $n_{N-1}$ local vector elements the following sub-matrix is stored:

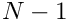
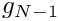
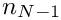
$\left[\begin{array}{cccccc} l_{(g_{N-1})} & d_{(g_{N-1}+1)} & u_{(g_{N-1}+1)} \\ & \ddots & \ddots & \ddots \\ & & & l_{(g_{N-1}+n_{N-1}-1)} & d_{(g_{N-1}+n_{N-1})} \end{array}\right].$

In this case, arrays lower[], diag[], and upper[] of dimension localDim, localDim and localDim-1 respectively are stored (see initialize()).

See the source code for this simple example by clicking on the link to the definition below.

Definition at line 107 of file ExampleTridiagSpmdLinearOp.hpp.

Constructor & Destructor Documentation

◆ ExampleTridiagSpmdLinearOp() [1/2]

template<class Scalar >

ExampleTridiagSpmdLinearOp< Scalar >::ExampleTridiagSpmdLinearOp ( )

inline

Construct to uninitialized.

Definition at line 111 of file ExampleTridiagSpmdLinearOp.hpp.

◆ ExampleTridiagSpmdLinearOp() [2/2]

template<class Scalar >

ExampleTridiagSpmdLinearOp< Scalar >::ExampleTridiagSpmdLinearOp	(	const Teuchos::RCP< const Teuchos::Comm< Thyra::Ordinal > > &	comm,
		const Thyra::Ordinal	localDim,
		const Teuchos::ArrayView< const Scalar > &	lower,
		const Teuchos::ArrayView< const Scalar > &	diag,
		const Teuchos::ArrayView< const Scalar > &	upper
	)

inline

Calls initialize().

Definition at line 114 of file ExampleTridiagSpmdLinearOp.hpp.

Member Function Documentation

◆ initialize()

template<class Scalar >

void ExampleTridiagSpmdLinearOp< Scalar >::initialize	(	const Teuchos::RCP< const Teuchos::Comm< Thyra::Ordinal > > &	comm,
		const Thyra::Ordinal	localDim,
		const Teuchos::ArrayView< const Scalar > &	lower,
		const Teuchos::ArrayView< const Scalar > &	diag,
		const Teuchos::ArrayView< const Scalar > &	upper
	)

Initialize given lower, diagonal and upper arrays of data.

Parameters

comm	[in] Communicator (allowed to be Teuchos::null)
localDim	[in] Dimension of this matrix (must be >= 2).
lower	[in] Array (length `( procRank == 0 ? localDim - 1 : localDim )`) of the lower diagonal elements
diag	[in] Array (length `localDim`) of the central diagonal elements
upper	[in] Array (length `( procRank == numProc-1 ? localDim - 1 : localDim )`) of the upper diagonal elements

Preconditions:

localDim >= 2

Postconditions:

Should be obvious!

Definition at line 196 of file ExampleTridiagSpmdLinearOp.hpp.

◆ range()

template<class Scalar >

Teuchos::RCP< const Thyra::VectorSpaceBase< Scalar > > ExampleTridiagSpmdLinearOp< Scalar >::range ( ) const

inlineprotectedvirtual

Implements Thyra::LinearOpBase< Scalar >.

Definition at line 157 of file ExampleTridiagSpmdLinearOp.hpp.

◆ domain()

template<class Scalar >

Teuchos::RCP< const Thyra::VectorSpaceBase< Scalar > > ExampleTridiagSpmdLinearOp< Scalar >::domain ( ) const

inlineprotectedvirtual

Implements Thyra::LinearOpBase< Scalar >.

Definition at line 161 of file ExampleTridiagSpmdLinearOp.hpp.

◆ opSupportedImpl()

template<class Scalar >

bool ExampleTridiagSpmdLinearOp< Scalar >::opSupportedImpl ( Thyra::EOpTransp M_trans ) const

inlineprotectedvirtual

Implements Thyra::LinearOpBase< Scalar >.

Definition at line 165 of file ExampleTridiagSpmdLinearOp.hpp.

◆ applyImpl()

template<class Scalar >

void ExampleTridiagSpmdLinearOp< Scalar >::applyImpl	(	const Thyra::EOpTransp	M_trans,
		const Thyra::MultiVectorBase< Scalar > &	X_in,
		const Teuchos::Ptr< Thyra::MultiVectorBase< Scalar > > &	Y_inout,
		const Scalar	alpha,
		const Scalar	beta
	)		const

protectedvirtual

Implements Thyra::LinearOpBase< Scalar >.

Definition at line 214 of file ExampleTridiagSpmdLinearOp.hpp.

The documentation for this class was generated from the following file:

ExampleTridiagSpmdLinearOp.hpp

Public Member Functions

Protected Member Functions

Additional Inherited Members

Detailed Description

Constructor & Destructor Documentation

◆ ExampleTridiagSpmdLinearOp() [1/2]

◆ ExampleTridiagSpmdLinearOp() [2/2]

Member Function Documentation

◆ initialize()

◆ range()

◆ domain()

◆ opSupportedImpl()

◆ applyImpl()