van der Pol model problem for nonlinear electrical circuit. More...

#include <VanDerPolModel_decl.hpp>

Inheritance diagram for Tempus_Test::VanDerPolModel< Scalar >:

Public Member Functions
	VanDerPolModel (Teuchos::RCP< Teuchos::ParameterList > pList=Teuchos::null)

Thyra::ModelEvaluatorBase::InArgs< Scalar >	getExactSolution (double t) const

Thyra::ModelEvaluatorBase::InArgs< Scalar >	getExactSensSolution (int j, double t) const

Private functions overridden from ModelEvaluatorDefaultBase.
int	dim_
	Number of state unknowns (2)

int	Np_
	Number of parameter vectors (1)

int	np_
	Number of parameters in this vector (1)

int	Ng_
	Number of observation functions (0)

int	ng_
	Number of elements in this observation function (0)

bool	haveIC_
	false => no nominal values are provided (default=true)

bool	acceptModelParams_
	Changes inArgs to require parameters.

bool	isInitialized_

Thyra::ModelEvaluatorBase::InArgs< Scalar >	inArgs_

Thyra::ModelEvaluatorBase::OutArgs< Scalar >	outArgs_

Thyra::ModelEvaluatorBase::InArgs< Scalar >	nominalValues_

Teuchos::RCP< const Thyra::VectorSpaceBase< Scalar > >	x_space_

Teuchos::RCP< const Thyra::VectorSpaceBase< Scalar > >	f_space_

Teuchos::RCP< const Thyra::VectorSpaceBase< Scalar > >	p_space_

Teuchos::RCP< const Thyra::VectorSpaceBase< Scalar > >	g_space_

Scalar	epsilon_
	This is a model parameter.

Scalar	t0_ic_
	initial time

Scalar	x0_ic_
	initial condition for x0

Scalar	x1_ic_
	initial condition for x1

Thyra::ModelEvaluatorBase::OutArgs< Scalar >	createOutArgsImpl () const

void	evalModelImpl (const Thyra::ModelEvaluatorBase::InArgs< Scalar > &inArgs_bar, const Thyra::ModelEvaluatorBase::OutArgs< Scalar > &outArgs_bar) const

Public functions overridden from ModelEvaluator.
Teuchos::RCP< const Thyra::VectorSpaceBase< Scalar > >	get_x_space () const

Teuchos::RCP< const Thyra::VectorSpaceBase< Scalar > >	get_f_space () const

Thyra::ModelEvaluatorBase::InArgs< Scalar >	getNominalValues () const

Teuchos::RCP< Thyra::LinearOpWithSolveBase< Scalar > >	create_W () const

Teuchos::RCP< Thyra::LinearOpBase< Scalar > >	create_W_op () const

Teuchos::RCP< const Thyra::LinearOpWithSolveFactoryBase< Scalar > >	get_W_factory () const

Thyra::ModelEvaluatorBase::InArgs< Scalar >	createInArgs () const

Teuchos::RCP< const Thyra::VectorSpaceBase< Scalar > >	get_p_space (int l) const

Teuchos::RCP< const Teuchos::Array< std::string > >	get_p_names (int l) const

Teuchos::RCP< const Thyra::VectorSpaceBase< Scalar > >	get_g_space (int j) const

Public functions overridden from ParameterListAcceptor.
void	setParameterList (Teuchos::RCP< Teuchos::ParameterList > const &paramList)

Teuchos::RCP< const Teuchos::ParameterList >	getValidParameters () const

void	setupInOutArgs_ () const

Detailed Description

template<class Scalar>
class Tempus_Test::VanDerPolModel< Scalar >

van der Pol model problem for nonlinear electrical circuit.

This is a canonical equation of a nonlinear oscillator (Hairer, Norsett, and Wanner, pp. 111-115, and Hairer and Wanner, pp. 4-5) for an electrical circuit. In implicit ODE form, 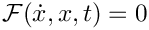$\mathcal{F}(\dot{x},x,t) = 0$ , the scaled problem can be written as

$\begin{eqnarray*} \mathcal{F}_0 & = & \dot{x}_0(t) - x_1(t) = 0 \\ \mathcal{F}_1 & = & \dot{x}_1(t) - [(1-x_0^2)x_1-x_0]/\epsilon = 0 \end{eqnarray*}$

where the initial conditions are

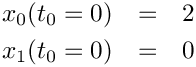
$\begin{eqnarray*} x_0(t_0=0) & = & 2 \\ x_1(t_0=0) & = & 0 \end{eqnarray*}$

and the initial time derivatives are

$\begin{eqnarray*} \dot{x}_0(t_0=0) & = & x_1(t_0=0) = 0 \\ \dot{x}_1(t_0=0) & = & [(1-x_0^2)x_1-x_0]/\epsilon = -2/\epsilon \end{eqnarray*}$

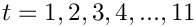
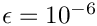
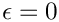
Hairer and Wanner suggest the output times of , and $\epsilon = 10^{-6}$ to make the problem very stiff. For $\epsilon = 0$ , the solution becomes

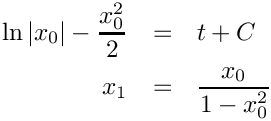
$\begin{eqnarray*} \ln \left|x_0\right| - \frac{x_0^2}{2} & = & t + C \\ x_1 & = & \frac{x_0}{1-x_0^2} \end{eqnarray*}$

where 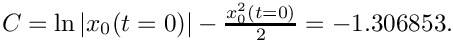$C =\ln \left|x_0(t=0)\right| - \frac{x_0^2(t=0)}{2} =-1.306853.$

The components of iteration matrix, , are defined to be

$W_{ij} \equiv \frac{d\mathcal{F}_i}{dx_j} = \frac{d}{dx_j} \mathcal{F}_i (\dot{x}_i, x_0, \ldots, x_k, \ldots, x_K, t)$

(not using Einstein summation). Using the chain rule, we can write

$\frac{d\mathcal{F}_i}{dx_j} = \frac{\partial\dot{x}_i}{\partial x_j} \frac{\partial\mathcal{F}_i}{\partial \dot{x}_i} + \sum_{k=0}^K \frac{\partial x_k}{\partial x_j} \frac{\partial\mathcal{F}_i}{\partial x_k} + \frac{\partial t}{\partial x_j} \frac{\partial\mathcal{F}_i}{\partial t}$

but noting that 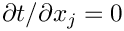$\partial t/\partial x_j = 0$ and

$\frac{\partial x_k}{\partial x_j} = \left\{ \begin{array}{c} 1 \mbox{ if } j = k \\ 0 \mbox{ if } j \neq k \end{array} \right.$

we can write

$\frac{d\mathcal{F}_i}{dx_j} = \alpha \frac{\partial\mathcal{F}_i}{\partial \dot{x}_j} + \beta \frac{\partial\mathcal{F}_i}{\partial x_j}$

where

$\alpha = \left\{ \begin{array}{cl} \frac{\partial\dot{x}_i}{\partial x_j} & \mbox{ if } i = j \\ 0 & \mbox{ if } i \neq j \end{array} \right. \;\;\;\; \mbox{ and } \;\;\;\; \beta = \left\{ \begin{array}{cl} \frac{\partial x_k}{\partial x_j} = 1 & \mbox{ if } j = k \\ 0 & \mbox{ if } j \neq k \end{array} \right.$

Thus for the van der Pol problem, we have

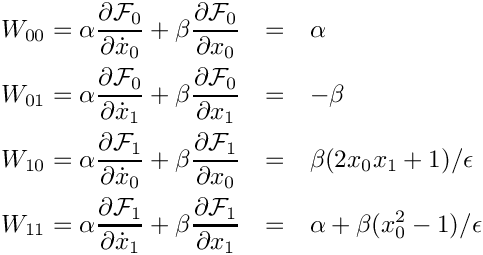
$\begin{eqnarray*} W_{00} = \alpha \frac{\partial\mathcal{F}_0}{\partial \dot{x}_0} + \beta \frac{\partial\mathcal{F}_0}{\partial x_0} & = & \alpha \\ W_{01} = \alpha \frac{\partial\mathcal{F}_0}{\partial \dot{x}_1} + \beta \frac{\partial\mathcal{F}_0}{\partial x_1} & = & -\beta \\ W_{10} = \alpha \frac{\partial\mathcal{F}_1}{\partial \dot{x}_0} + \beta \frac{\partial\mathcal{F}_1}{\partial x_0} & = & \beta (2 x_0 x_1 + 1)/\epsilon \\ W_{11} = \alpha \frac{\partial\mathcal{F}_1}{\partial \dot{x}_1} + \beta \frac{\partial\mathcal{F}_1}{\partial x_1} & = & \alpha + \beta (x^2_0 - 1)/\epsilon \\ \end{eqnarray*}$

Definition at line 112 of file VanDerPolModel_decl.hpp.

Constructor & Destructor Documentation

◆ VanDerPolModel()

template<class Scalar >

Tempus_Test::VanDerPolModel< Scalar >::VanDerPolModel ( Teuchos::RCP< Teuchos::ParameterList > pList = Teuchos::null )

Definition at line 28 of file VanDerPolModel_impl.hpp.

Member Function Documentation

◆ getExactSolution()

template<class Scalar >

Thyra::ModelEvaluatorBase::InArgs< Scalar > Tempus_Test::VanDerPolModel< Scalar >::getExactSolution ( double t ) const

Definition at line 56 of file VanDerPolModel_impl.hpp.

◆ getExactSensSolution()

template<class Scalar >

Thyra::ModelEvaluatorBase::InArgs< Scalar > Tempus_Test::VanDerPolModel< Scalar >::getExactSensSolution	(	int	j,
		double	t
	)		const

Definition at line 66 of file VanDerPolModel_impl.hpp.

◆ get_x_space()

template<class Scalar >

Teuchos::RCP< const Thyra::VectorSpaceBase< Scalar > > Tempus_Test::VanDerPolModel< Scalar >::get_x_space ( ) const

Definition at line 76 of file VanDerPolModel_impl.hpp.

◆ get_f_space()

template<class Scalar >

Teuchos::RCP< const Thyra::VectorSpaceBase< Scalar > > Tempus_Test::VanDerPolModel< Scalar >::get_f_space ( ) const

Definition at line 83 of file VanDerPolModel_impl.hpp.

◆ getNominalValues()

template<class Scalar >

Thyra::ModelEvaluatorBase::InArgs< Scalar > Tempus_Test::VanDerPolModel< Scalar >::getNominalValues ( ) const

Definition at line 90 of file VanDerPolModel_impl.hpp.

◆ create_W()

template<class Scalar >

Teuchos::RCP< Thyra::LinearOpWithSolveBase< Scalar > > Tempus_Test::VanDerPolModel< Scalar >::create_W ( ) const

Definition at line 99 of file VanDerPolModel_impl.hpp.

◆ create_W_op()

template<class Scalar >

Teuchos::RCP< Thyra::LinearOpBase< Scalar > > Tempus_Test::VanDerPolModel< Scalar >::create_W_op ( ) const

Definition at line 137 of file VanDerPolModel_impl.hpp.

◆ get_W_factory()

template<class Scalar >

Teuchos::RCP< const Thyra::LinearOpWithSolveFactoryBase< Scalar > > Tempus_Test::VanDerPolModel< Scalar >::get_W_factory ( ) const

Definition at line 147 of file VanDerPolModel_impl.hpp.

◆ createInArgs()

template<class Scalar >

Thyra::ModelEvaluatorBase::InArgs< Scalar > Tempus_Test::VanDerPolModel< Scalar >::createInArgs ( ) const

Definition at line 155 of file VanDerPolModel_impl.hpp.

◆ get_p_space()

template<class Scalar >

Teuchos::RCP< const Thyra::VectorSpaceBase< Scalar > > Tempus_Test::VanDerPolModel< Scalar >::get_p_space ( int l ) const

Definition at line 273 of file VanDerPolModel_impl.hpp.

◆ get_p_names()

template<class Scalar >

Teuchos::RCP< const Teuchos::Array< std::string > > Tempus_Test::VanDerPolModel< Scalar >::get_p_names ( int l ) const

Definition at line 284 of file VanDerPolModel_impl.hpp.

◆ get_g_space()

template<class Scalar >

Teuchos::RCP< const Thyra::VectorSpaceBase< Scalar > > Tempus_Test::VanDerPolModel< Scalar >::get_g_space ( int j ) const

Definition at line 298 of file VanDerPolModel_impl.hpp.

◆ setParameterList()

template<class Scalar >

void Tempus_Test::VanDerPolModel< Scalar >::setParameterList ( Teuchos::RCP< Teuchos::ParameterList > const & paramList )

Definition at line 375 of file VanDerPolModel_impl.hpp.

◆ getValidParameters()

template<class Scalar >

Teuchos::RCP< const Teuchos::ParameterList > Tempus_Test::VanDerPolModel< Scalar >::getValidParameters ( ) const

Definition at line 402 of file VanDerPolModel_impl.hpp.

◆ setupInOutArgs_()

template<class Scalar >

void Tempus_Test::VanDerPolModel< Scalar >::setupInOutArgs_ ( ) const

private

Definition at line 307 of file VanDerPolModel_impl.hpp.

◆ createOutArgsImpl()

template<class Scalar >

Thyra::ModelEvaluatorBase::OutArgs< Scalar > Tempus_Test::VanDerPolModel< Scalar >::createOutArgsImpl ( ) const

private

Definition at line 166 of file VanDerPolModel_impl.hpp.

◆ evalModelImpl()

template<class Scalar >

void Tempus_Test::VanDerPolModel< Scalar >::evalModelImpl	(	const Thyra::ModelEvaluatorBase::InArgs< Scalar > &	inArgs_bar,
		const Thyra::ModelEvaluatorBase::OutArgs< Scalar > &	outArgs_bar
	)		const

private

Definition at line 173 of file VanDerPolModel_impl.hpp.

Member Data Documentation

◆ dim_

template<class Scalar >

int Tempus_Test::VanDerPolModel< Scalar >::dim_

private

Number of state unknowns (2)

Definition at line 160 of file VanDerPolModel_decl.hpp.

◆ Np_

template<class Scalar >

int Tempus_Test::VanDerPolModel< Scalar >::Np_

private

Number of parameter vectors (1)

Definition at line 161 of file VanDerPolModel_decl.hpp.

◆ np_

template<class Scalar >

int Tempus_Test::VanDerPolModel< Scalar >::np_

private

Number of parameters in this vector (1)

Definition at line 162 of file VanDerPolModel_decl.hpp.

◆ Ng_

template<class Scalar >

int Tempus_Test::VanDerPolModel< Scalar >::Ng_

private

Number of observation functions (0)

Definition at line 163 of file VanDerPolModel_decl.hpp.

◆ ng_

template<class Scalar >

int Tempus_Test::VanDerPolModel< Scalar >::ng_

private

Number of elements in this observation function (0)

Definition at line 164 of file VanDerPolModel_decl.hpp.

◆ haveIC_

template<class Scalar >

bool Tempus_Test::VanDerPolModel< Scalar >::haveIC_

private

false => no nominal values are provided (default=true)

Definition at line 165 of file VanDerPolModel_decl.hpp.

◆ acceptModelParams_

template<class Scalar >

bool Tempus_Test::VanDerPolModel< Scalar >::acceptModelParams_

private

Changes inArgs to require parameters.

Definition at line 166 of file VanDerPolModel_decl.hpp.

◆ isInitialized_

template<class Scalar >

bool Tempus_Test::VanDerPolModel< Scalar >::isInitialized_

mutableprivate

Definition at line 167 of file VanDerPolModel_decl.hpp.

◆ inArgs_

template<class Scalar >

Thyra::ModelEvaluatorBase::InArgs<Scalar> Tempus_Test::VanDerPolModel< Scalar >::inArgs_

mutableprivate

Definition at line 168 of file VanDerPolModel_decl.hpp.

◆ outArgs_

template<class Scalar >

Thyra::ModelEvaluatorBase::OutArgs<Scalar> Tempus_Test::VanDerPolModel< Scalar >::outArgs_

mutableprivate

Definition at line 169 of file VanDerPolModel_decl.hpp.

◆ nominalValues_

template<class Scalar >

Thyra::ModelEvaluatorBase::InArgs<Scalar> Tempus_Test::VanDerPolModel< Scalar >::nominalValues_

mutableprivate

Definition at line 170 of file VanDerPolModel_decl.hpp.

◆ x_space_

template<class Scalar >

Teuchos::RCP<const Thyra::VectorSpaceBase<Scalar> > Tempus_Test::VanDerPolModel< Scalar >::x_space_

private

Definition at line 171 of file VanDerPolModel_decl.hpp.

◆ f_space_

template<class Scalar >

Teuchos::RCP<const Thyra::VectorSpaceBase<Scalar> > Tempus_Test::VanDerPolModel< Scalar >::f_space_

private

Definition at line 172 of file VanDerPolModel_decl.hpp.

◆ p_space_

template<class Scalar >

Teuchos::RCP<const Thyra::VectorSpaceBase<Scalar> > Tempus_Test::VanDerPolModel< Scalar >::p_space_

private

Definition at line 173 of file VanDerPolModel_decl.hpp.

◆ g_space_

template<class Scalar >

Teuchos::RCP<const Thyra::VectorSpaceBase<Scalar> > Tempus_Test::VanDerPolModel< Scalar >::g_space_

private

Definition at line 174 of file VanDerPolModel_decl.hpp.

◆ epsilon_

template<class Scalar >

Scalar Tempus_Test::VanDerPolModel< Scalar >::epsilon_

private

This is a model parameter.

Definition at line 177 of file VanDerPolModel_decl.hpp.

◆ t0_ic_

template<class Scalar >

Scalar Tempus_Test::VanDerPolModel< Scalar >::t0_ic_

private

initial time

Definition at line 178 of file VanDerPolModel_decl.hpp.

◆ x0_ic_

template<class Scalar >

Scalar Tempus_Test::VanDerPolModel< Scalar >::x0_ic_

private

initial condition for x0

Definition at line 179 of file VanDerPolModel_decl.hpp.

◆ x1_ic_

template<class Scalar >

Scalar Tempus_Test::VanDerPolModel< Scalar >::x1_ic_

private

initial condition for x1

Definition at line 180 of file VanDerPolModel_decl.hpp.

The documentation for this class was generated from the following files:

Public Member Functions

Private functions overridden from ModelEvaluatorDefaultBase.

Public functions overridden from ModelEvaluator.

Public functions overridden from ParameterListAcceptor.

Detailed Description

Constructor & Destructor Documentation

◆ VanDerPolModel()

Member Function Documentation

◆ getExactSolution()

◆ getExactSensSolution()

◆ get_x_space()

◆ get_f_space()

◆ getNominalValues()

◆ create_W()

◆ create_W_op()

◆ get_W_factory()

◆ createInArgs()

◆ get_p_space()

◆ get_p_names()

◆ get_g_space()

◆ setParameterList()

◆ getValidParameters()

◆ setupInOutArgs_()

◆ createOutArgsImpl()

◆ evalModelImpl()

Member Data Documentation

◆ dim_

◆ Np_

◆ np_

◆ Ng_

◆ ng_

◆ haveIC_

◆ acceptModelParams_

◆ isInitialized_

◆ inArgs_

◆ outArgs_

◆ nominalValues_

◆ x_space_

◆ f_space_

◆ p_space_

◆ g_space_

◆ epsilon_

◆ t0_ic_

◆ x0_ic_

◆ x1_ic_