Class representing an exponential covariance function and its KL eigevalues/eigenfunctions. More...

#include <Stokhos_KL_OneDExponentialCovarianceFunction.hpp>

Classes
struct	EigFuncCos
	Nonlinear function whose roots define eigenvalues for cos() eigenfunction. More...

struct	EigFuncSin
	Nonlinear function whose roots define eigenvalues for sin() eigenfunction. More...

Public Types
typedef ExponentialOneDEigenFunction< value_type >	eigen_function_type

typedef OneDEigenPair< eigen_function_type >	eigen_pair_type

Public Member Functions
	OneDExponentialCovarianceFunction (int M, const value_type &a, const value_type &b, const value_type &L, const int dim_name, Teuchos::ParameterList &solverParams)
	Constructor.

	~OneDExponentialCovarianceFunction ()
	Destructor.

value_type	evaluateCovariance (const value_type &x, const value_type &xp) const
	Evaluate covariance.

const Teuchos::Array< eigen_pair_type > &	getEigenPairs () const
	Get eigenpairs.

Protected Types
typedef Teuchos::ScalarTraits< value_type >::magnitudeType	magnitude_type

Protected Member Functions
template<class Func >
value_type	newton (const Func &func, const value_type &a, const value_type &b, magnitude_type tol, int max_num_its)
	A basic root finder based on Newton's method.

template<class Func >
value_type	bisection (const Func &func, const value_type &a, const value_type &b, magnitude_type tol, int max_num_its)
	A basic root finder based on bisection.

Protected Attributes
value_type	L
	Correlation length.

Teuchos::Array< eigen_pair_type >	eig_pair
	Eigenpairs.

Detailed Description

template<typename value_type>
class Stokhos::KL::OneDExponentialCovarianceFunction< value_type >

Class representing an exponential covariance function and its KL eigevalues/eigenfunctions.

This class provides the exponential covariance function

$\mbox{cov}(x,x') = \exp(-|x-x'|/L).$

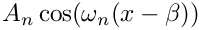
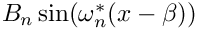
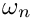
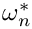
The corresponding eigenfunctions can be shown to be $A_n\cos(\omega_n(x-\beta))$ and $B_n\sin(\omega^\ast_n(x-\beta))$ for $x\in[a,b]$ where $\omega_n$ and $\omega^\ast_n$ satisfy

$1 - L\omega_n\tan(\omega_n\alpha) = 0$

and

$L\omega^\ast_n + \tan(\omega^\ast_n\alpha) = 0$

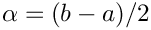
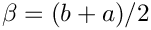
respectively, where $\alpha=(b-a)/2$ and $\beta=(b+a)/2$ . Then

$A_n = \frac{1}{\left(\int_a^b\cos^2(\omega_n(x-\beta)) dx\right)^{1/2}} = \frac{1}{\sqrt{\alpha + \frac{\sin(2\omega_n\alpha)}{2\omega_n}}},$

$B_n = \frac{1}{\left(\int_a^b\sin^2(\omega^\ast_n(x-\beta)) dx\right)^{1/2}} = \frac{1}{\sqrt{\alpha - \frac{\sin(2\omega_n^\ast\alpha)}{2\omega^\ast_n}}}$

and the corresponding eigenvalues are given by

$\lambda_n = \frac{2L}{(L\omega_n)^2 + 1}$

and

$\lambda^\ast_n = \frac{2L}{(L\omega^\ast_n)^2 + 1}.$

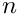
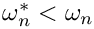
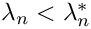
It is straightforward to show that for each , $\omega^\ast_n < \omega_n$ , and thus $\lambda_n < \lambda^\ast_n$ . Hence when sorted on decreasing eigenvalue, the eigenfunctions alternate between cosine and sine. See "Stochastic Finite Elements" by Ghanem and Spanos for a complete description of how to derive these relationships.

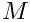
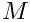
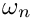
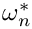
For a given value of , the code works by computing the eigenfunctions using a bisection root solver to compute the frequencies $\omega_n$ and $\omega^\ast_n$ .

Data for the root solver is passed through a Teuchos::ParameterList, which accepts the following parameters:

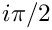
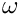
"Bound Peturbation Size" – [value_type] (1.0e-6) Perturbation away from $i\pi/2$ for bounding the frequencies $\omega$ in the bisection algorithm
"Nonlinear Solver Tolerance" – [value_type] (1.0e-10) Tolerance for bisection nonlinear solver for computing frequencies
"Maximum Nonlinear Solver Iterations" – [int] (100) Maximum number of nonlinear solver iterations for computing the frequencies.

The documentation for this class was generated from the following files:

Stokhos_KL_OneDExponentialCovarianceFunction.hpp
Stokhos_KL_OneDExponentialCovarianceFunctionImp.hpp

Classes

Public Types

Public Member Functions

Protected Types

Protected Member Functions

Protected Attributes

Detailed Description