Common line search utilites for computing the slope of a function. More...
#include <NOX_LineSearch_Utils_Slope.H>
Public Member Functions | |
| Slope () | |
| Constructor (requires call to reset() to initialize object). | |
| Slope (const Teuchos::RCP< NOX::GlobalData > &gd) | |
| Constructor. | |
| virtual | ~Slope () |
| Destructor. | |
| void | reset (const Teuchos::RCP< NOX::GlobalData > &gd) |
| Reset method. | |
| double | computeSlope (const NOX::Abstract::Vector &dir, const NOX::Abstract::Group &grp) |
| Compute the inner product of the given direction and the gradient associated with the given group. | |
| double | computeSlopeWithOutJac (const NOX::Abstract::Vector &dir, const NOX::Abstract::Group &grp) |
| This is a variant of the computeSlope() method above optimized to work with out having to compute an explicit Jacobian. | |
Detailed Description
Common line search utilites for computing the slope of a function.
This class provides routines for computing the slope of a give function. There are two methods, one that uses a Jacobian and the other that estimates the action of the Jacobian by directional derivatives.
Member Function Documentation
◆ computeSlope()
| double NOX::LineSearch::Utils::Slope::computeSlope | ( | const NOX::Abstract::Vector & | dir, |
| const NOX::Abstract::Group & | grp | ||
| ) |
Compute the inner product of the given direction and the gradient associated with the given group.
Calculates and returns
![\[
\zeta = d^T \nabla f(x).
\]](form_177.png)
Here 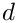
dir and 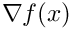
References NOX::Abstract::Group::applyJacobian(), NOX::Abstract::Vector::clone(), NOX::Abstract::Group::getF(), NOX::Abstract::Group::getGradient(), NOX::Abstract::Vector::innerProduct(), NOX::Abstract::Group::isF(), NOX::Abstract::Group::isGradient(), NOX::Abstract::Group::Ok, and NOX::ShapeCopy.
◆ computeSlopeWithOutJac()
| double NOX::LineSearch::Utils::Slope::computeSlopeWithOutJac | ( | const NOX::Abstract::Vector & | dir, |
| const NOX::Abstract::Group & | grp | ||
| ) |
This is a variant of the computeSlope() method above optimized to work with out having to compute an explicit Jacobian.
Calculates and returns
\f[
\zeta = d^T \nabla f(x) = d^TJ^TF
\f]
Here \f$d\f$ represents the input parameter \c dir \f$\nabla
f(x)\f$ is the gradient associated with the given group (for nonlinear solves this equates to \f$ J^TF \f$ where \f$ J \f$ is the Jacobian and \f$ F \f$ is the original nonlinear function).
We can rewrite this equation as:
\f[ d^TJ^TF = F^TJd \f]
which allows us to use directional derivatives to estimate \f$ J^TF \f$:
\f[ F^TJd = F^T \frac{F(x + \eta d) - F(x)}{\eta} \f]
This may allow for faster computations of the slope if the Jacobian is expensive to evaluate.
where 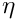
![\[ \eta = \lambda * (\lambda + \frac{\| x\|}{\| d\|} ) \]](form_179.png)
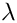
References NOX::Abstract::Group::clone(), NOX::Abstract::Vector::clone(), NOX::Abstract::Group::getF(), NOX::Abstract::Group::getX(), NOX::Abstract::Group::isF(), NOX::Abstract::Vector::norm(), and NOX::ShapeCopy.
The documentation for this class was generated from the following files:
- NOX_LineSearch_Utils_Slope.H
- NOX_LineSearch_Utils_Slope.C