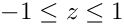Compute the value of the i th Lagrangian interpolant through the np Gauss-Jacobi/Gauss-Radau-Jacobi/Gauss-Lobatto points zgj at the arbitrary location z. More...
#include <Intrepid2_Polylib.hpp>
Public Member Functions | |
| KOKKOS_INLINE_FUNCTION zViewType::value_type | getValue (const ordinal_type i, const typename zViewType::value_type z, const zViewType zgj, const ordinal_type np, const double alpha, const double beta) |
| KOKKOS_INLINE_FUNCTION zViewType::value_type | getValue (const ordinal_type i, const typename zViewType::value_type z, const zViewType zgrj, const ordinal_type np, const double alpha, const double beta) |
| KOKKOS_INLINE_FUNCTION zViewType::value_type | getValue (const ordinal_type i, const typename zViewType::value_type z, const zViewType zgrj, const ordinal_type np, const double alpha, const double beta) |
| KOKKOS_INLINE_FUNCTION zViewType::value_type | getValue (const ordinal_type i, const typename zViewType::value_type z, const zViewType zglj, const ordinal_type np, const double alpha, const double beta) |
Detailed Description
template<EPolyType polyType>
struct Intrepid2::Polylib::Serial::LagrangianInterpolant< polyType >
struct Intrepid2::Polylib::Serial::LagrangianInterpolant< polyType >
Compute the value of the i th Lagrangian interpolant through the np Gauss-Jacobi/Gauss-Radau-Jacobi/Gauss-Lobatto points zgj at the arbitrary location z.
- POLYTYPE_GAUSS Uses the defintion of the Lagrangian interpolant:
![$
\begin{array}{rcl}
h_j(z) = \left\{ \begin{array}{ll}
\displaystyle \frac{P_{np}^{\alpha,\beta}(z)}
{[P_{np}^{\alpha,\beta}(z_j)]^\prime
(z-z_j)} & \mbox{if $z \ne z_j$}\\
& \\
1 & \mbox{if $z=z_j$}
\end{array}
\right.
\end{array}
$](form_315.png)
![$
\begin{array}{rcl}
h_j(z) = \left\{ \begin{array}{ll}
\displaystyle \frac{P_{np}^{\alpha,\beta}(z)}
{[P_{np}^{\alpha,\beta}(z_j)]^\prime
(z-z_j)} & \mbox{if $z \ne z_j$}\\
& \\
1 & \mbox{if $z=z_j$}
\end{array}
\right.
\end{array}
$](form_315_dark.png)
- Gauss-Radau-Jacobi (Left) Uses the defintion of the Lagrangian interpolant:
%![$ \begin{array}{rcl}
h_j(z) = \left\{ \begin{array}{ll}
\displaystyle \frac{(1+z) P_{np-1}^{\alpha,\beta+1}(z)}
{((1+z_j) [P_{np-1}^{\alpha,\beta+1}(z_j)]^\prime +
P_{np-1}^{\alpha,\beta+1}(z_j) ) (z-z_j)} & \mbox{if $z \ne z_j$}\\
& \\
1 & \mbox{if $z=z_j$}
\end{array}
\right.
\end{array} $](form_316.png)
![$ \begin{array}{rcl}
h_j(z) = \left\{ \begin{array}{ll}
\displaystyle \frac{(1+z) P_{np-1}^{\alpha,\beta+1}(z)}
{((1+z_j) [P_{np-1}^{\alpha,\beta+1}(z_j)]^\prime +
P_{np-1}^{\alpha,\beta+1}(z_j) ) (z-z_j)} & \mbox{if $z \ne z_j$}\\
& \\
1 & \mbox{if $z=z_j$}
\end{array}
\right.
\end{array} $](form_316_dark.png)
- Gauss-Radau-Jacobi (Right) Uses the defintion of the Lagrangian interpolant:
%![$ \begin{array}{rcl}
h_j(z) = \left\{ \begin{array}{ll}
\displaystyle \frac{(1-z) P_{np-1}^{\alpha+1,\beta}(z)}
{((1-z_j) [P_{np-1}^{\alpha+1,\beta}(z_j)]^\prime -
P_{np-1}^{\alpha+1,\beta}(z_j) ) (z-z_j)} & \mbox{if $z \ne z_j$}\\
& \\
1 & \mbox{if $z=z_j$}
\end{array}
\right.
\end{array} $](form_317.png)
![$ \begin{array}{rcl}
h_j(z) = \left\{ \begin{array}{ll}
\displaystyle \frac{(1-z) P_{np-1}^{\alpha+1,\beta}(z)}
{((1-z_j) [P_{np-1}^{\alpha+1,\beta}(z_j)]^\prime -
P_{np-1}^{\alpha+1,\beta}(z_j) ) (z-z_j)} & \mbox{if $z \ne z_j$}\\
& \\
1 & \mbox{if $z=z_j$}
\end{array}
\right.
\end{array} $](form_317_dark.png)
- Gauss-Lobatto Uses the defintion of the Lagrangian interpolant:
%![$ \begin{array}{rcl}
h_j(z) = \left\{ \begin{array}{ll}
\displaystyle \frac{(1-z^2) P_{np-2}^{\alpha+1,\beta+1}(z)}
{((1-z^2_j) [P_{np-2}^{\alpha+1,\beta+1}(z_j)]^\prime -
2 z_j P_{np-2}^{\alpha+1,\beta+1}(z_j) ) (z-z_j)}&\mbox{if $z \ne z_j$}\\
& \\
1 & \mbox{if $z=z_j$}
\end{array}
\right.
\end{array} $](form_318.png)
![$ \begin{array}{rcl}
h_j(z) = \left\{ \begin{array}{ll}
\displaystyle \frac{(1-z^2) P_{np-2}^{\alpha+1,\beta+1}(z)}
{((1-z^2_j) [P_{np-2}^{\alpha+1,\beta+1}(z_j)]^\prime -
2 z_j P_{np-2}^{\alpha+1,\beta+1}(z_j) ) (z-z_j)}&\mbox{if $z \ne z_j$}\\
& \\
1 & \mbox{if $z=z_j$}
\end{array}
\right.
\end{array} $](form_318_dark.png)
Definition at line 350 of file Intrepid2_Polylib.hpp.
Member Function Documentation
◆ getValue() [1/4]
| KOKKOS_INLINE_FUNCTION zViewType::value_type Intrepid2::Polylib::Serial::LagrangianInterpolant< POLYTYPE_GAUSS >::getValue | ( | const ordinal_type | i, |
| const typename zViewType::value_type | z, | ||
| const zViewType | zgj, | ||
| const ordinal_type | np, | ||
| const double | alpha, | ||
| const double | beta | ||
| ) |
Definition at line 398 of file Intrepid2_PolylibDef.hpp.
◆ getValue() [2/4]
| KOKKOS_INLINE_FUNCTION zViewType::value_type Intrepid2::Polylib::Serial::LagrangianInterpolant< POLYTYPE_GAUSS_LOBATTO >::getValue | ( | const ordinal_type | i, |
| const typename zViewType::value_type | z, | ||
| const zViewType | zglj, | ||
| const ordinal_type | np, | ||
| const double | alpha, | ||
| const double | beta | ||
| ) |
Definition at line 507 of file Intrepid2_PolylibDef.hpp.
◆ getValue() [3/4]
| KOKKOS_INLINE_FUNCTION zViewType::value_type Intrepid2::Polylib::Serial::LagrangianInterpolant< POLYTYPE_GAUSS_RADAU_LEFT >::getValue | ( | const ordinal_type | i, |
| const typename zViewType::value_type | z, | ||
| const zViewType | zgrj, | ||
| const ordinal_type | np, | ||
| const double | alpha, | ||
| const double | beta | ||
| ) |
Definition at line 431 of file Intrepid2_PolylibDef.hpp.
◆ getValue() [4/4]
| KOKKOS_INLINE_FUNCTION zViewType::value_type Intrepid2::Polylib::Serial::LagrangianInterpolant< POLYTYPE_GAUSS_RADAU_RIGHT >::getValue | ( | const ordinal_type | i, |
| const typename zViewType::value_type | z, | ||
| const zViewType | zgrj, | ||
| const ordinal_type | np, | ||
| const double | alpha, | ||
| const double | beta | ||
| ) |
Definition at line 469 of file Intrepid2_PolylibDef.hpp.
The documentation for this struct was generated from the following file:
- /home/runner/work/trilinos.github.io/trilinos.github.io/Trilinos/packages/intrepid2/src/Shared/Intrepid2_Polylib.hpp
