An implementation of the Anasazi::GenOrthoManager that performs orthogonalization using iterated classical Gram-Schmidt. More...

#include <AnasaziICGSOrthoManager.hpp>

Inheritance diagram for Anasazi::ICGSOrthoManager< ScalarType, MV, OP >:

Public Member Functions
Constructor/Destructor
	ICGSOrthoManager (Teuchos::RCP< const OP > Op=Teuchos::null, int numIters=2, typename Teuchos::ScalarTraits< ScalarType >::magnitudeType eps=0.0, typename Teuchos::ScalarTraits< ScalarType >::magnitudeType tol=0.20)
	Constructor specifying the operator defining the inner product as well as the number of orthogonalization iterations.

	~ICGSOrthoManager ()
	Destructor.

Methods implementing Anasazi::GenOrthoManager
void	projectGen (MV &S, Teuchos::Array< Teuchos::RCP< const MV > > X, Teuchos::Array< Teuchos::RCP< const MV > > Y, bool isBiOrtho, Teuchos::Array< Teuchos::RCP< Teuchos::SerialDenseMatrix< int, ScalarType > > > C=Teuchos::tuple(Teuchos::RCP< Teuchos::SerialDenseMatrix< int, ScalarType > >(Teuchos::null)), Teuchos::RCP< MV > MS=Teuchos::null, Teuchos::Array< Teuchos::RCP< const MV > > MX=Teuchos::tuple(Teuchos::RCP< const MV >(Teuchos::null)), Teuchos::Array< Teuchos::RCP< const MV > > MY=Teuchos::tuple(Teuchos::RCP< const MV >(Teuchos::null))) const
	Applies a series of generic projectors.

int	projectAndNormalizeGen (MV &S, Teuchos::Array< Teuchos::RCP< const MV > > X, Teuchos::Array< Teuchos::RCP< const MV > > Y, bool isBiOrtho, Teuchos::Array< Teuchos::RCP< Teuchos::SerialDenseMatrix< int, ScalarType > > > C=Teuchos::tuple(Teuchos::RCP< Teuchos::SerialDenseMatrix< int, ScalarType > >(Teuchos::null)), Teuchos::RCP< Teuchos::SerialDenseMatrix< int, ScalarType > > B=Teuchos::null, Teuchos::RCP< MV > MS=Teuchos::null, Teuchos::Array< Teuchos::RCP< const MV > > MX=Teuchos::tuple(Teuchos::RCP< const MV >(Teuchos::null)), Teuchos::Array< Teuchos::RCP< const MV > > MY=Teuchos::tuple(Teuchos::RCP< const MV >(Teuchos::null))) const
	Applies a series of generic projectors and returns an orthonormal basis for the residual data.

Methods implementing Anasazi::MatOrthoManager
void	projectMat (MV &X, Teuchos::Array< Teuchos::RCP< const MV > > Q, Teuchos::Array< Teuchos::RCP< Teuchos::SerialDenseMatrix< int, ScalarType > > > C=Teuchos::tuple(Teuchos::RCP< Teuchos::SerialDenseMatrix< int, ScalarType > >(Teuchos::null)), Teuchos::RCP< MV > MX=Teuchos::null, Teuchos::Array< Teuchos::RCP< const MV > > MQ=Teuchos::tuple(Teuchos::RCP< const MV >(Teuchos::null))) const
	Given a list of mutually orthogonal and internally orthonormal bases `Q`, this method projects a multivector `X` onto the space orthogonal to the individual `Q[i]`, optionally returning the coefficients of `X` for the individual `Q[i]`. All of this is done with respect to the inner product innerProd().

int	normalizeMat (MV &X, Teuchos::RCP< Teuchos::SerialDenseMatrix< int, ScalarType > > B=Teuchos::null, Teuchos::RCP< MV > MX=Teuchos::null) const
	This method takes a multivector `X` and attempts to compute an orthonormal basis for , with respect to innerProd().

int	projectAndNormalizeMat (MV &X, Teuchos::Array< Teuchos::RCP< const MV > > Q, Teuchos::Array< Teuchos::RCP< Teuchos::SerialDenseMatrix< int, ScalarType > > > C=Teuchos::tuple(Teuchos::RCP< Teuchos::SerialDenseMatrix< int, ScalarType > >(Teuchos::null)), Teuchos::RCP< Teuchos::SerialDenseMatrix< int, ScalarType > > B=Teuchos::null, Teuchos::RCP< MV > MX=Teuchos::null, Teuchos::Array< Teuchos::RCP< const MV > > MQ=Teuchos::tuple(Teuchos::RCP< const MV >(Teuchos::null))) const
	Given a set of bases `Q[i]` and a multivector `X`, this method computes an orthonormal basis for $colspan(X) - \sum_i colspan(Q[i])$ .

Error methods
Teuchos::ScalarTraits< ScalarType >::magnitudeType	orthonormErrorMat (const MV &X, Teuchos::RCP< const MV > MX=Teuchos::null) const
	This method computes the error in orthonormality of a multivector, measured as the Frobenius norm of the difference `innerProd(X,Y) - I`. The method has the option of exploiting a caller-provided `MX`.

Teuchos::ScalarTraits< ScalarType >::magnitudeType	orthogErrorMat (const MV &X1, const MV &X2, Teuchos::RCP< const MV > MX1, Teuchos::RCP< const MV > MX2) const
	This method computes the error in orthogonality of two multivectors, measured as the Frobenius norm of `innerProd(X,Y)`. The method has the option of exploiting a caller-provided `MX`.

Public Member Functions inherited from Anasazi::GenOrthoManager< ScalarType, MV, OP >
	GenOrthoManager (Teuchos::RCP< const OP > Op=Teuchos::null)
	Default constructor.

virtual	~GenOrthoManager ()
	Destructor.

Public Member Functions inherited from Anasazi::MatOrthoManager< ScalarType, MV, OP >
	MatOrthoManager (Teuchos::RCP< const OP > Op=Teuchos::null)
	Default constructor.

virtual	~MatOrthoManager ()
	Destructor.

virtual void	setOp (Teuchos::RCP< const OP > Op)
	Set operator used for inner product.

virtual Teuchos::RCP< const OP >	getOp () const
	Get operator used for inner product.

int	getOpCounter () const
	Retrieve operator counter.

void	resetOpCounter ()
	Reset the operator counter to zero.

void	innerProdMat (const MV &X, const MV &Y, Teuchos::SerialDenseMatrix< int, ScalarType > &Z, Teuchos::RCP< const MV > MX=Teuchos::null, Teuchos::RCP< const MV > MY=Teuchos::null) const
	Provides a matrix-based inner product.

void	normMat (const MV &X, std::vector< typename Teuchos::ScalarTraits< ScalarType >::magnitudeType > &normvec, Teuchos::RCP< const MV > MX=Teuchos::null) const
	Provides the norm induced by the matrix-based inner product.

void	innerProd (const MV &X, const MV &Y, Teuchos::SerialDenseMatrix< int, ScalarType > &Z) const
	Implements the interface OrthoManager::innerProd().

void	norm (const MV &X, std::vector< typename Teuchos::ScalarTraits< ScalarType >::magnitudeType > &normvec) const
	Implements the interface OrthoManager::norm().

void	project (MV &X, Teuchos::Array< Teuchos::RCP< const MV > > Q, Teuchos::Array< Teuchos::RCP< Teuchos::SerialDenseMatrix< int, ScalarType > > > C=Teuchos::tuple(Teuchos::RCP< Teuchos::SerialDenseMatrix< int, ScalarType > >(Teuchos::null))) const
	Implements the interface OrthoManager::project().

int	normalize (MV &X, Teuchos::RCP< Teuchos::SerialDenseMatrix< int, ScalarType > > B=Teuchos::null) const
	Implements the interface OrthoManager::normalize().

int	projectAndNormalize (MV &X, Teuchos::Array< Teuchos::RCP< const MV > > Q, Teuchos::Array< Teuchos::RCP< Teuchos::SerialDenseMatrix< int, ScalarType > > > C=Teuchos::tuple(Teuchos::RCP< Teuchos::SerialDenseMatrix< int, ScalarType > >(Teuchos::null)), Teuchos::RCP< Teuchos::SerialDenseMatrix< int, ScalarType > > B=Teuchos::null) const
	Implements the interface OrthoManager::projectAndNormalize().

Teuchos::ScalarTraits< ScalarType >::magnitudeType	orthonormError (const MV &X) const
	Implements the interface OrthoManager::orthonormError().

Teuchos::ScalarTraits< ScalarType >::magnitudeType	orthogError (const MV &X1, const MV &X2) const
	Implements the interface OrthoManager::orthogError().

Public Member Functions inherited from Anasazi::OrthoManager< ScalarType, MV >
	OrthoManager ()
	Default constructor.

virtual	~OrthoManager ()
	Destructor.

Accessor routines
void	setNumIters (int numIters)
	Set parameter for re-orthogonalization threshold.

int	getNumIters () const
	Return parameter for re-orthogonalization threshold.

Additional Inherited Members
Protected Attributes inherited from Anasazi::MatOrthoManager< ScalarType, MV, OP >

Detailed Description

template<class ScalarType, class MV, class OP>
class Anasazi::ICGSOrthoManager< ScalarType, MV, OP >

An implementation of the Anasazi::GenOrthoManager that performs orthogonalization using iterated classical Gram-Schmidt.

Author: Chris Baker, Ulrich Hetmaniuk, Rich Lehoucq, and Heidi Thornquist

Definition at line 39 of file AnasaziICGSOrthoManager.hpp.

Constructor & Destructor Documentation

◆ ICGSOrthoManager()

template<class ScalarType , class MV , class OP >

Anasazi::ICGSOrthoManager< ScalarType, MV, OP >::ICGSOrthoManager	(	Teuchos::RCP< const OP >	Op = `Teuchos::null`,
		int	numIters = `2`,
		typename Teuchos::ScalarTraits< ScalarType >::magnitudeType	eps = `0.0`,
		typename Teuchos::ScalarTraits< ScalarType >::magnitudeType	tol = `0.20`
	)

Constructor specifying the operator defining the inner product as well as the number of orthogonalization iterations.

Definition at line 379 of file AnasaziICGSOrthoManager.hpp.

◆ ~ICGSOrthoManager()

template<class ScalarType , class MV , class OP >

Anasazi::ICGSOrthoManager< ScalarType, MV, OP >::~ICGSOrthoManager ( )

inline

Destructor.

Definition at line 58 of file AnasaziICGSOrthoManager.hpp.

Member Function Documentation

◆ projectGen()

template<class ScalarType , class MV , class OP >

void Anasazi::ICGSOrthoManager< ScalarType, MV, OP >::projectGen	(	MV &	S,
		Teuchos::Array< Teuchos::RCP< const MV > >	X,
		Teuchos::Array< Teuchos::RCP< const MV > >	Y,
		bool	isBiOrtho,
		Teuchos::Array< Teuchos::RCP< Teuchos::SerialDenseMatrix< int, ScalarType > > >	C = `Teuchos::tuple(Teuchos::RCP< Teuchos::SerialDenseMatrix<int,ScalarType> >(Teuchos::null))`,
		Teuchos::RCP< MV >	MS = `Teuchos::null`,
		Teuchos::Array< Teuchos::RCP< const MV > >	MX = `Teuchos::tuple(Teuchos::RCP<const MV>(Teuchos::null))`,
		Teuchos::Array< Teuchos::RCP< const MV > >	MY = `Teuchos::tuple(Teuchos::RCP<const MV>(Teuchos::null))`
	)		const

virtual

Applies a series of generic projectors.

Given a list of bases X[i] and Y[i] (a projection pair), this method takes a multivector S and applies the projectors

$P_{X[i],Y[i]} S = S - X[i] \langle Y[i], X[i] \rangle^{-1} \langle Y[i], S \rangle\ .$

This operation projects S onto the space orthogonal to the Y[i], along the range of the X[i]. The inner product specified by 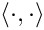$\langle \cdot, \cdot \rangle$ is given by innerProd().

Note: The call
projectGen(S, tuple(X1,X2), tuple(Y1,Y2))

Anasazi::ICGSOrthoManager::projectGen
void projectGen(MV &S, Teuchos::Array< Teuchos::RCP< const MV > > X, Teuchos::Array< Teuchos::RCP< const MV > > Y, bool isBiOrtho, Teuchos::Array< Teuchos::RCP< Teuchos::SerialDenseMatrix< int, ScalarType > > > C=Teuchos::tuple(Teuchos::RCP< Teuchos::SerialDenseMatrix< int, ScalarType > >(Teuchos::null)), Teuchos::RCP< MV > MS=Teuchos::null, Teuchos::Array< Teuchos::RCP< const MV > > MX=Teuchos::tuple(Teuchos::RCP< const MV >(Teuchos::null)), Teuchos::Array< Teuchos::RCP< const MV > > MY=Teuchos::tuple(Teuchos::RCP< const MV >(Teuchos::null))) const
Applies a series of generic projectors.
Definition AnasaziICGSOrthoManager.hpp:515

is equivalent to the call
projectGen(S, tuple(X2,X1), tuple(Y2,Y1))

The method also returns the coefficients C[i] associated with each projection pair, so that

$S_{in} = S_{out} + \sum_i X[i] C[i]$

and therefore

$C[i] = \langle Y[i], X[i] \rangle^{-1} \langle Y[i], S \rangle\ .$

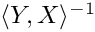
Lastly, for reasons of efficiency, the user must specify whether the projection pairs are bi-orthonormal with respect to innerProd(), i.e., whether $\langle Y[i], X[i] \rangle = I$ . In the case that the bases are specified to be biorthogonal, the inverse $\langle Y, X \rangle^{-1}$ will not be computed. Furthermore, the user may optionally specifiy the image of S and the projection pairs under the inner product operator getOp().

projectGen() is implemented to apply the projectors via an iterated Classical Gram-Schmidt, where the iteration is performed getNumIters() number of times.

Parameters

S	[in/out] The multivector to be modified. On output, the columns of `S` will be orthogonal to each `Y[i]`, satisfying $\langle Y[i], S_{out} \rangle = 0$ Also, $S_{in} = S_{out} + \sum_i X[i] C[i]$
X	[in] Multivectors for bases under which 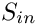$S_{in}$ is modified.
Y	[in] Multivectors for bases to which 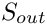$S_{out}$ should be orthogonal.
isBiortho	[in] A flag specifying whether the bases `X[i]` and `Y[i]` are biorthonormal, i.e,. whether $\langle Y[i], X[i]\rangle == I$ .
C	[out] Coefficients for reconstructing 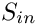$S_{in}$ via the bases `X[i]`. If `C[i]` is a non-null pointer and `C[i]` matches the dimensions of `S` and `X[i]`, then the coefficients computed during the orthogonalization routine will be stored in the matrix `C[i]`. If `C[i]` points to a Teuchos::SerialDenseMatrix with size inconsistent with `S` and `X[i]`, then a std::invalid_argument exception will be thrown. Otherwise, if `C.size() < i` or `C[i]` is a null pointer, the caller will not have access to the computed coefficients `C[i]`.
MS	[in/out] If specified by the user, on input `MS` is required to be the image of `S` under the operator getOp(). On output, `MS` will be updated to reflect the changes in `S`.
MX	[in] If specified by the user, on `MX[i]` is required to be the image of `X[i]` under the operator getOp().
MY	[in] If specified by the user, on `MY[i]` is required to be the image of `Y[i]` under the operator getOp().

Precondition

If X[i] != Teuchos::null or Y[i] != Teuchos::null, then X[i] and Y[i] are required to have the same number of columns, and each should have the same number of rows as S.
For any i != j, $\langle Y[i], X[j] \rangle == 0$ .
If biOrtho == true, $\langle Y[i], X[i]\rangle == I$
Otherwise, if biOrtho == false, then $\langle Y[i], X[i]\rangle$ should be Hermitian positive-definite.
If X[i] and Y[i] have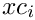 columns and S has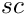 columns, then C[i] if specified must be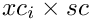 $xc_i \times sc$ .

Implements Anasazi::GenOrthoManager< ScalarType, MV, OP >.

Definition at line 515 of file AnasaziICGSOrthoManager.hpp.

◆ projectAndNormalizeGen()

template<class ScalarType , class MV , class OP >

int Anasazi::ICGSOrthoManager< ScalarType, MV, OP >::projectAndNormalizeGen	(	MV &	S,
		Teuchos::Array< Teuchos::RCP< const MV > >	X,
		Teuchos::Array< Teuchos::RCP< const MV > >	Y,
		bool	isBiOrtho,
		Teuchos::Array< Teuchos::RCP< Teuchos::SerialDenseMatrix< int, ScalarType > > >	C = `Teuchos::tuple(Teuchos::RCP< Teuchos::SerialDenseMatrix<int,ScalarType> >(Teuchos::null))`,
		Teuchos::RCP< Teuchos::SerialDenseMatrix< int, ScalarType > >	B = `Teuchos::null`,
		Teuchos::RCP< MV >	MS = `Teuchos::null`,
		Teuchos::Array< Teuchos::RCP< const MV > >	MX = `Teuchos::tuple(Teuchos::RCP<const MV>(Teuchos::null))`,
		Teuchos::Array< Teuchos::RCP< const MV > >	MY = `Teuchos::tuple(Teuchos::RCP<const MV>(Teuchos::null))`
	)		const

virtual

Applies a series of generic projectors and returns an orthonormal basis for the residual data.

Given a list of bases X[i] and Y[i] (a projection pair), this method takes a multivector S and applies the projectors

$P_{X[i],Y[i]} S = S - X[i] \langle Y[i], X[i] \rangle^{-1} \langle Y[i], S \rangle\ .$

These operation project S onto the space orthogonal to the range of the Y[i], along the range of X[i]. The inner product specified by 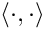$\langle \cdot, \cdot \rangle$ is given by innerProd().

The method returns in S an orthonormal basis for the residual

$\left( \prod_{i} P_{X[i],Y[i]} \right) S_{in} = S_{out} B\ ,$

where B contains the (not necessarily triangular) coefficients of the residual with respect to the new basis.

The method also returns the coefficients C[i] and B associated with each projection pair, so that

$S_{in} = S_{out} B + \sum_i X[i] C[i]$

and

$C[i] = \langle Y[i], X[i] \rangle^{-1} \langle Y[i], S \rangle\ .$

Lastly, for reasons of efficiency, the user must specify whether the projection pairs are bi-orthonormal with respect to innerProd(), i.e., whether $\langle Y[i], X[i] \rangle = I$ . Furthermore, the user may optionally specifiy the image of S and the projection pairs under the inner product operator getOp().

Parameters

S	[in/out] The multivector to be modified. On output, the columns of `S` will be orthogonal to each `Y[i]`, satisfying $\langle Y[i], S_{out} \rangle = 0$ Also, $S_{in}(1:m,1:n) = S_{out}(1:m,1:rank) B(1:rank,1:n) + \sum_i X[i] C[i]\ ,$ where `m` is the number of rows in `S`, `n` is the number of columns in `S`, and `rank` is the value returned from the method.
X	[in] Multivectors for bases under which 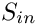$S_{in}$ is modified.
Y	[in] Multivectors for bases to which 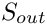$S_{out}$ should be orthogonal.
isBiortho	[in] A flag specifying whether the bases `X[i]` and `Y[i]` are biorthonormal, i.e,. whether $\langle Y[i], X[i]\rangle == I$ .
C	[out] Coefficients for reconstructing 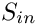$S_{in}$ via the bases `X[i]`. If `C[i]` is a non-null pointer and `C[i]` matches the dimensions of `X` and `Q[i]`, then the coefficients computed during the orthogonalization routine will be stored in the matrix `C[i]`. If `C[i]` points to a Teuchos::SerialDenseMatrix with size inconsistent with `S` and `X[i]`, then a std::invalid_argument exception will be thrown. Otherwise, if `C.size() < i` or `C[i]` is a null pointer, the caller will not have access to the computed coefficients `C[i]`.
B	[out] The coefficients of the original `S` with respect to the computed basis. If `B` is a non-null pointer and `B` matches the dimensions of `B`, then the coefficients computed during the orthogonalization routine will be stored in `B`, similar to calling innerProd( Sout, Sin, B ); Anasazi::MatOrthoManager::innerProd void innerProd(const MV &X, const MV &Y, Teuchos::SerialDenseMatrix< int, ScalarType > &Z) const Implements the interface OrthoManager::innerProd(). Definition AnasaziMatOrthoManager.hpp:315 If `B` points to a Teuchos::SerialDenseMatrix with size inconsistent with `S`, then a std::invalid_argument exception will be thrown. Otherwise, if `B` is null, the caller will not have access to the computed coefficients. The normalization uses classical Gram-Schmidt iteration, so that `B` is an upper triangular matrix with positive diagonal elements.
MS	[in/out] If specified by the user, on input `MS` is required to be the image of `S` under the operator getOp(). On output, `MS` will be updated to reflect the changes in `S`.
MX	[in] If specified by the user, on `MX[i]` is required to be the image of `X[i]` under the operator getOp().
MY	[in] If specified by the user, on `MY[i]` is required to be the image of `Y[i]` under the operator getOp().

Precondition

If X[i] != Teuchos::null or Y[i] != Teuchos::null, then X[i] and Y[i] are required to have the same number of columns, and each should have the same number of rows as S.
For any i != j, $\langle Y[i], X[j] \rangle == 0$ .
If biOrtho == true, $\langle Y[i], X[i]\rangle == I$
Otherwise, if biOrtho == false, then $\langle Y[i], X[i]\rangle$ should be Hermitian positive-definite.
If X[i] and Y[i] have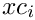 columns and S has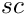 columns, then C[i] if specified must be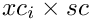 $xc_i \times sc$ .
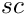
If S has columns, then B if specified must be $sc \times sc$ .

Returns: Rank of the basis computed by this method.

Implements Anasazi::GenOrthoManager< ScalarType, MV, OP >.

Definition at line 860 of file AnasaziICGSOrthoManager.hpp.

◆ projectMat()

template<class ScalarType , class MV , class OP >

void Anasazi::ICGSOrthoManager< ScalarType, MV, OP >::projectMat	(	MV &	X,
		Teuchos::Array< Teuchos::RCP< const MV > >	Q,
		Teuchos::Array< Teuchos::RCP< Teuchos::SerialDenseMatrix< int, ScalarType > > >	C = `Teuchos::tuple(Teuchos::RCP< Teuchos::SerialDenseMatrix<int,ScalarType> >(Teuchos::null))`,
		Teuchos::RCP< MV >	MX = `Teuchos::null`,
		Teuchos::Array< Teuchos::RCP< const MV > >	MQ = `Teuchos::tuple(Teuchos::RCP<const MV>(Teuchos::null))`
	)		const

virtual

Given a list of mutually orthogonal and internally orthonormal bases Q, this method projects a multivector X onto the space orthogonal to the individual Q[i], optionally returning the coefficients of X for the individual Q[i]. All of this is done with respect to the inner product innerProd().

This method calls projectGen() as follows:

projectGen(X,Q,Q,true,C,MX,MQ,MQ);

See projectGen() for argument requirements.

Implements Anasazi::MatOrthoManager< ScalarType, MV, OP >.

Definition at line 434 of file AnasaziICGSOrthoManager.hpp.

◆ normalizeMat()

template<class ScalarType , class MV , class OP >

int Anasazi::ICGSOrthoManager< ScalarType, MV, OP >::normalizeMat	(	MV &	X,
		Teuchos::RCP< Teuchos::SerialDenseMatrix< int, ScalarType > >	B = `Teuchos::null`,
		Teuchos::RCP< MV >	MX = `Teuchos::null`
	)		const

virtual

This method takes a multivector X and attempts to compute an orthonormal basis for 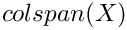, with respect to innerProd().

This method calls projectAndNormalizeGen() as follows:

projectAndNormalizeGen(X,empty,empty,true,empty,B,MX);

Anasazi::ICGSOrthoManager::projectAndNormalizeGen

int projectAndNormalizeGen(MV &S, Teuchos::Array< Teuchos::RCP< const MV > > X, Teuchos::Array< Teuchos::RCP< const MV > > Y, bool isBiOrtho, Teuchos::Array< Teuchos::RCP< Teuchos::SerialDenseMatrix< int, ScalarType > > > C=Teuchos::tuple(Teuchos::RCP< Teuchos::SerialDenseMatrix< int, ScalarType > >(Teuchos::null)), Teuchos::RCP< Teuchos::SerialDenseMatrix< int, ScalarType > > B=Teuchos::null, Teuchos::RCP< MV > MS=Teuchos::null, Teuchos::Array< Teuchos::RCP< const MV > > MX=Teuchos::tuple(Teuchos::RCP< const MV >(Teuchos::null)), Teuchos::Array< Teuchos::RCP< const MV > > MY=Teuchos::tuple(Teuchos::RCP< const MV >(Teuchos::null))) const

Applies a series of generic projectors and returns an orthonormal basis for the residual data.

Definition AnasaziICGSOrthoManager.hpp:860

See projectAndNormalizeGen() for argument requirements.

Implements Anasazi::MatOrthoManager< ScalarType, MV, OP >.

Definition at line 450 of file AnasaziICGSOrthoManager.hpp.

◆ projectAndNormalizeMat()

template<class ScalarType , class MV , class OP >

int Anasazi::ICGSOrthoManager< ScalarType, MV, OP >::projectAndNormalizeMat	(	MV &	X,
		Teuchos::Array< Teuchos::RCP< const MV > >	Q,
		Teuchos::Array< Teuchos::RCP< Teuchos::SerialDenseMatrix< int, ScalarType > > >	C = `Teuchos::tuple(Teuchos::RCP< Teuchos::SerialDenseMatrix<int,ScalarType> >(Teuchos::null))`,
		Teuchos::RCP< Teuchos::SerialDenseMatrix< int, ScalarType > >	B = `Teuchos::null`,
		Teuchos::RCP< MV >	MX = `Teuchos::null`,
		Teuchos::Array< Teuchos::RCP< const MV > >	MQ = `Teuchos::tuple(Teuchos::RCP<const MV>(Teuchos::null))`
	)		const

virtual

Given a set of bases Q[i] and a multivector X, this method computes an orthonormal basis for $colspan(X) - \sum_i colspan(Q[i])$ .

This method calls projectAndNormalizeGen() as follows:

projectAndNormalizeGen(X,Q,Q,true,C,B,MX,MQ,MQ);

See projectAndNormalizeGen() for argument requirements.

Implements Anasazi::MatOrthoManager< ScalarType, MV, OP >.

Definition at line 499 of file AnasaziICGSOrthoManager.hpp.

◆ orthonormErrorMat()

template<class ScalarType , class MV , class OP >

Teuchos::ScalarTraits< ScalarType >::magnitudeType Anasazi::ICGSOrthoManager< ScalarType, MV, OP >::orthonormErrorMat	(	const MV &	X,
		Teuchos::RCP< const MV >	MX = `Teuchos::null`
	)		const

virtual

This method computes the error in orthonormality of a multivector, measured as the Frobenius norm of the difference innerProd(X,Y) - I. The method has the option of exploiting a caller-provided MX.

Implements Anasazi::MatOrthoManager< ScalarType, MV, OP >.

Definition at line 405 of file AnasaziICGSOrthoManager.hpp.

◆ orthogErrorMat()

template<class ScalarType , class MV , class OP >

Teuchos::ScalarTraits< ScalarType >::magnitudeType Anasazi::ICGSOrthoManager< ScalarType, MV, OP >::orthogErrorMat	(	const MV &	X1,
		const MV &	X2,
		Teuchos::RCP< const MV >	MX1,
		Teuchos::RCP< const MV >	MX2
	)		const

virtual

This method computes the error in orthogonality of two multivectors, measured as the Frobenius norm of innerProd(X,Y). The method has the option of exploiting a caller-provided MX.

Implements Anasazi::MatOrthoManager< ScalarType, MV, OP >.

Definition at line 422 of file AnasaziICGSOrthoManager.hpp.