This file first gives an example of how to create an Epetra_CrsMatrix object, then it details the supported matrices and gives a list of required parameters.

Given an already created Epetra_Map, Galeri can construct an Epetra_CrsMatrix object that has this Map as RowMatrixRowMap(). A simple example is as follows. Let Map be an already created Epetra_Map* object; then, a diagonal matrix with 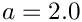on the diagonal can be created using the instructions

#include "Galeri_CrsMatrices.h"
using namespace Galeri;
...
string MatrixType = "Diag";
List.set("a", 2.0);
Epetra_CrsMatrix* Matrix = CreateCrsMatrix(MatrixType, Map, List);

More interesting matrices can be easily created. For example, a 2D biharmonic operator can be created like this:

List.set("nx", 10);
List.set("ny", 10);
Epetra_CrsMatrix* Matrix = Galeri.Create("Biharmonic2D", Map, List);

For matrices arising from 2D discretizations on Cartesian grids, it is possible to visualize the computational stencil at a given grid point by using function PrintStencil2D, defined in the Galeri namespace:

#include "Galeri_Utils.h"
using namespace Galeri;
...
// Matrix is an already created Epetra_CrsMatrix* object
// and nx and ny the number of nodes along the X-axis and Y-axis, 
// respectively.
PrintStencil2D(Matrix, nx, ny);

The output is:

2D computational stencil at GID 12 (grid is 5 x 5)

        0          0          1          0          0
        0          2         -8          2          0
        1         -8         20         -8          1
        0          2         -8          2          0
        0          0          1          0          0

To present the list of supported matrices we adopt the following symbols:

MATLAB: please refer to the MATLAB documentation for more details on the properties of this matrix;
DENSE: the matrix is dense (but still stored as Epetra_CrsMatrix);
MAP: the number of elements and its distribution are determined from the input map;
MAP2D: the input map has been created by CreateMap(), using MapType = Cartesian2D. The values of nx and ny are still available in the input list;
MAP3D: the input map has been created by CreateMap(), using MapType = Cartesian3D. The values of nx, ny and nz are still available in the input list;
SER: the matrix can be obtained in serial environments only;
PAR: the matrix can be obtained in parallel (and serial) environments.
The symbol $A_{i,j}$ indicates the matrix of the element in MATLAB notation (that is, starting from 1).

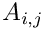
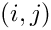
The list of supported matrices is now reported in alphabetical order.

BentPipe2D (MAP2D, PAR): Returns a matrix corresponding to the finite-difference discretization of the problem
$- \epsilon \Delta u + (v_x,v_y) \cdot \nabla u = f$
on the unit square, with homogeneous Dirichlet boundary conditions. A standard 5-pt stencil is used to discretize the diffusive term, and a simple upwind stencil is used for the convective term. Here,
$v_x = 2 conv x (x/2 - 1) (1 - 2y), \quad \quad \quad v_y =-4 conv y (y - 1) (1 - x)$
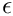
The value of $\epsilon$ can be specified using diff, and that of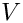 using conv. The default values are diff=1e-5, conv=1.
BigCross2D (MAP2D, PAR): Creates a matrix corresponding to the following stencil:
$\left[ \begin{tabular}{ccccc} & & ee & & \\ & & e & & \\ bb & b & a & c & cc \\ & & d & & \\ & & dd & & \\ \end{tabular} \right] .$
The default values are those given by Laplace2DFourthOrder. A non-default value must be set in the input parameter list before creating the matrix. For example, to specify the value of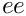 , one should do
```
  List.set("ee", 12.0);
  Matrix = Galeri.Create("BigCross2D", Map, List);
```
BigStar2D (MAP2D, PAR): Creates a matrix corresponding to the stencil
$\left[ \begin{tabular}{ccccc} & & ee & & \\ & z3 & e & z4 & \\ bb & b & a & c & cc \\ & z1 & d & z2 & \\ & & dd & & \\ \end{tabular} \right] .$
The default values are those given by Biharmonic2D.
Biharmonic2D (MAP2D, PAR): Creates a matrix corresponding to the discrete biharmonic operator,
$\frac{1}{h^4} \; \left[ \begin{tabular}{ccccc} & & 1 & & \\ & 2 & -8 & 2 & \\ 1 & -8 & 20 & -8 & 1 \\ & 2 & -8 & 2 & \\ & & 1 & & \\ \end{tabular} \right] .$
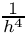
The formula does not include the $\frac{1}{h^4}$ scaling.
Cauchy (MAP, MATLAB, DENSE, PAR): Creates a particular instance of a Cauchy matrix with elements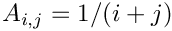 $A_{i,j} = 1/(i+j)$ . Explicit formulas are known for the inverse and determinant of a Cauchy matrix. For this particular Cauchy matrix, the determinant is nonzero and the matrix is totally positive.
Cross2D (MAP2D, PAR): Creates a matrix with the same stencil of Laplace2D}, but with arbitrary values. The computational stencil is
$\left[ \begin{tabular}{ccc} & e & \\ b & a & c \\ & d & \\ \end{tabular} \right] .$

The default values are
```
  List.set("a", 4.0);
  List.set("b", -1.0);
  List.set("c", -1.0);
  List.set("d", -1.0);
  List.set("e", -1.0);
```
For example, to approximate the 2D Helmhotlz equation
$- \nabla u - \sigma u = f \quad \quad (\sigma \geq 0)$

with the standard 5-pt discretization stencil
$\frac{1}{h^2} \; \left[ \begin{tabular}{ccc} & -1 & \\ -1 & $4 -\sigma h^2$ & -1 \\ & -1 & \\ \end{tabular} \right]$

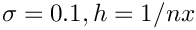
and $\sigma = 0.1, h = 1/nx$ , one can set
```
  List.set("a", 4 - 0.1 * h * h);
  List.set("b", -1.0);
  List.set("c", -1.0);
  List.set("d", -1.0);
  List.set("e", -1.0);
```
The factor $\frac{1}{h^2}$ can be considered by scaling the input parameters.
Cross3D (MAP3D, PAR): Similar to the Cross2D case. The matrix stencil correspond to that of a 3D Laplace operator on a structured 3D grid. On a given x-y plane, the stencil is as in Laplace2D. The value on the plane below is set using f, the value on the plane above with g.
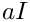
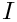
Diag (MAP, PAR): Creates , where is the identity matrix of size n. The default value is
```
  List.set("a", 1.0);
```
Fiedler (MAP, MATLAB, DENSE, PAR): Creates a matrix whose element are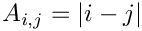 $A_{i,j} = | i - j |$ . The matrix is symmetric, and has a dominant positive eigenvalue, and all the other eigenvalues are negative.
Hanowa (MAP, MATLAB, PAR): Creates a matrix whose eigenvalues lie on a vertical line in the complex plane. The matrix has the 2x2 block structure (in MATLAB's notation)
$A = \left[ \begin{tabular}{cc} a * eye(n/2) & -diag(1:m) \\ diag(1:m) & a * eye(n/2) \\ \end{tabular} \right].$
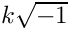
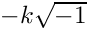
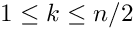
The complex eigenvalues are of the form a $k \sqrt{-1}$ and $-k \sqrt{-1}$ , for $1 \leq k \leq n/2$ . The default value is
```
List.set("a", -1.0);
```
Hilbert (MAP, MATLAB, DENSE, PAR): This is a famous example of a badly conditioned matrix. The elements are defined in MATLAB notation as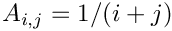 $A_{i,j} = 1/(i+j)$ .
JordanBlock (MAP, MATLAB, PAR): Creates a Jordan block with eigenvalue lambda. The default value is lambda=0.1;
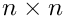
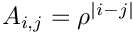
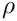
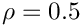
KMS (MAP, MATLAB, DENSE, PAR): Create the $n \times n$ Kac-Murdock-Szego Toepliz matrix such that $A_{i,j} = \rho^{|i-j|}$ (for real $\rho$ only). Default value is $\rho= 0.5$ , or can be using rho. The inverse of this matrix is tridiagonal, and the matrix is positive definite if and only if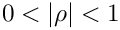 $0 < |\rho| < 1$ . The default value is rho=-0.5;
Laplace1D (MAP, PAR): Creates the classical tridiagonal matrix with stencil .
Laplace1DNeumann (MAP, PAR): As for Laplace1D, but with Neumann boundary conditioners. The matrix is singular.
Laplace2D (MAP2D, PAR): Creates a matrix corresponding to the stencil of a 2D Laplacian operator on a structured Cartesian grid. The matrix stencil is:
$\frac{1}{h^2} \; \left[ \begin{tabular}{ccc} & -1 & \\ -1 & 4 & -1 \\ & -1 & \\ \end{tabular} \right] .$
The formula does not include the $\frac{1}{h^2}$ scaling.
Laplace2DFourthOrder (MAP2D, PAR): Creates a matrix corresponding to the stencil of a 2D Laplacian operator on a structured Cartesian grid. The matrix stencil is:
$\frac{1}{12 h^2} \; \left[ \begin{tabular}{ccccc} & & 1 & & \\ & & -16 & & \\ 1 & -16 & 60 & -16 & 1 \\ & & -16 & & \\ & & 1 & & \\ \end{tabular} \right] .$
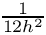
The formula does not include the $\frac{1}{12h^2}$ scaling.
Laplace3D (MAP3D, PAR): Creates a matrix corresponding to the stencil of a 3D Laplacian operator on a structured Cartesian grid.
Lehmer (MAP, MATLAB, DENSE, PAR): Returns a symmetric positive definite matrix, such that
$A_{i,j} = \left\{ \begin{array}{ll} \frac{i}{j} & \mbox{ if } j \ge i \\ \frac{j}{i} & \mbox{ otherwise } \\ \end{array} \right. .$
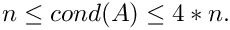
This matrix has three properties: is totally nonnegative, the inverse is tridiagonal and explicitly known, The condition number is bounded as $n \le cond(A) \le 4*n.$
Minij (MAP, MATLAB, DENSE, PAR): Returns the symmetric positive definite matrix defined as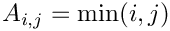 $A_{i,j} = \min(i,j)$ .
Ones (MAP, PAR): Returns a matrix with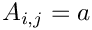 $A_{i,j} = a$ . The default value is a=1;
Parter (MAP, MATLAB, DENSE, PAR): Creates a matrix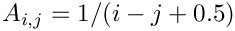 $A_{i,j} = 1/(i-j+0.5)$ . This matrix is a Cauchy and a Toepliz matrix. Most of the singular values of A are very close to $\pi$ .
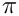
Pei (MAP, MATLAB, DENSE, PAR): Creates the matrix
$A_{i,j} = \left\{ \begin{array}{cc} \alpha + 1 & \mbox{ if } i \neq j \\ 1 & \mbox{ if } i = j. \end{array} \right. .$
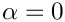
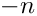
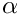
This matrix is singular for $\alpha = 0$ or . The default value for $\alpha$ is 1.0.
Recirc2D (MAP2D, PAR): Returns a matrix corresponding to the finite-difference discretization of the problem
$- \epsilon \Delta u + (v_x,v_y) \cdot \nabla u = f$
on the unit square, with homogeneous Dirichlet boundary conditions. A standard 5-pt stencil is used to discretize the diffusive term, and a simple upwind stencil is used for the convective term. Here,
$v_x = conv \cdot 4 x (x - 1) (1 - 2y), \quad \quad \quad v_y = -conv \cdot 4 y (y - 1) (1 - 2x)$
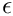
The value of $\epsilon$ can be specified using diff, and that of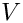 using conv. The default values are diff=1e-5, conv=1.
Ris (MAP, MATLAB, PAR): Returns a symmetric Hankel matrix with elements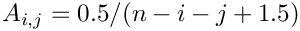 $A_{i,j} = 0.5/(n-i-j+1.5)$ , where is problem size. The eigenvalues of A cluster around $-\pi/2$ and $\pi/2$ .

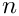
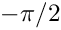
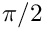
Star2D (MAP2D, PAR): Creates a matrix with the 9-point stencil:

$\left[ \begin{tabular}{ccc} z3 & e & z4 \\ b & a & c \\ z1 & d & z2 \\ \end{tabular} \right] .$

The default values are

  List.set("a", 8.0);
  List.set("b", -1.0);
  List.set("c", -1.0);
  List.set("d", -1.0);
  List.set("e", -1.0);
  List.set("z1", -1.0);
  List.set("z2", -1.0);
  List.set("z3", -1.0);
  List.set("z4", -1.0);

Stretched2D (MAP2D, PAR): Creates a matrix corresponding to the following stencil:
$\left[ \begin{tabular}{ccc} -1.0 & $-4.0 + \epsilon$ & -1.0 \\ $2.0 - \epsilon$ & 8.0 & $2.0 - \epsilon$ \\ -1.0 & $-4.0 + \epsilon$ & -1.0 \\ \end{tabular} \right] .$
This matrix corresponds to a 2D discretization of a Laplace operator using bilinear elements on a stretched grid. The default value is epsilon=0.1;
Tridiag (MAP, PAR): Creates a tridiagonal matrix with stencil
$\left[ \begin{tabular}{ccc} b & a & c \\ \end{tabular} \right] .$
The default values are
```
  List.set("a", 2.0);
  List.set("b", -1.0);
  List.set("c", -1.0);
```
UniFlow2D (MAP2D, PAR): Returns a matrix corresponding to the finite-difference discretization of the problem
$- \epsilon \Delta u + (v_x,v_y) \cdot \nabla u = f$
on the unit square, with homogeneous Dirichlet boundary conditions. A standard 5-pt stencil is used to discretize the diffusive term, and a simple upwind stencil is used for the convective term. Here,
$v_x = cos(\alpha) V, \quad \quad \quad v_y = sin(\alpha) V$
that corresponds to an unidirectional 2D flow. The default values are
```
    List.set("alpha", .0);
    List.set("diff", 1e-5);
    List.set("conv", 1.0);
```