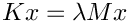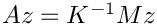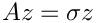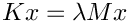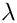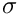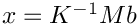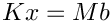BlockKrylovSchur/BlockKrylovSchurEpetraExGenAmesos.cpp

Compute smallest eigenvalues of a generalized eigenvalue problem, using block Krylov-Schur with Epetra and an Amesos direct solver.

Compute smallest eigenvalues of a generalized eigenvalue problem, using block Krylov-Schur with Epetra and an Amesos direct solver.This example computes the eigenvalues of smallest magnitude of a generalized eigenvalue problem , using Anasazi's implementation of the block Krylov-Schur method, with Epetra linear algebra and a direct solver from the Amesos package.

Anasazi computes the smallest-magnitude eigenvalues using a shift-and-invert strategy. For simplicity, this example uses a shift of zero. It illustrates the general pattern for using Anasazi for this problem:

1. Construct an "operator" A such that .
2. Use Anasazi to solve , which is a spectral transformation of the original problem .
3. The eigenvalues of the original problem are the inverses of the eigenvalues of the transformed problem.

In the example, the "operator A such that \f$A z = K^{-1} M z\f$" is a subclass of Epetra_Operator. The Apply method of that operator takes the vector b, and computes . It does so first by applying the matrix M, and then by solving the linear system for x. Trilinos implements many different ways to solve linear systems. The example uses the sparse direct solver KLU to do so. Trilinos' Amesos package has an interface to KLU.

// @HEADER
// *****************************************************************************
//                 Anasazi: Block Eigensolvers Package
//
// Copyright 2004 NTESS and the Anasazi contributors.
// SPDX-License-Identifier: BSD-3-Clause
// *****************************************************************************
// @HEADER
// This example computes the eigenvalues of smallest magnitude of a
// generalized eigenvalue problem $K x = \lambda M x$, using Anasazi's
// implementation of the block Krylov-Schur method.  It implements
// inverse iteration using the KLU sparse direct linear solver, and
// accesses KLU through Trilinos' Amesos package.
//
// Anasazi computes the smallest-magnitude eigenvalues using a
// shift-and-invert strategy.  For simplicity, the code below uses a
// shift of zero.  It illustrates the general pattern for using
// Anasazi for this problem:
//
//   1. Construct an "operator" A such that $Az = K^{-1} M z$.
//   2. Use Anasazi to solve $Az = \sigma z$, which is a spectral
//      transformation of the original problem $K x = \lambda M x$.
//   3. The eigenvalues $\lambda$ of the original problem are the
//      inverses of the eigenvalues $\sigma$ of the transformed
//      problem.
//
// The "operator A such that $A z = K^{-1} M z$" is a subclass of
// Epetra_Operator.  The Apply method of that operator takes the
// vector b, and computes $x = K^{-1} M b$.  It does so first by
// applying the matrix M, and then by solving the linear system $K x =
// M b$ for x.  Trilinos implements many different ways to solve
// linear systems.  The example below uses the sparse direct solver
// KLU to do so.  Trilinos' Amesos package has an interface to KLU.
 
// Include header for block Krylov-Schur solver
#include "AnasaziBlockKrylovSchurSolMgr.hpp"
// Include header to define basic eigenproblem Ax = \lambda*Bx
#include "AnasaziBasicEigenproblem.hpp"
// Include header to provide Anasazi with Epetra adapters.  If you
// plan to use Tpetra objects instead of Epetra objects, include
// AnasaziTpetraAdapter.hpp instead; do analogously if you plan to use
// Thyra objects instead of Epetra objects.
#include "AnasaziEpetraAdapter.hpp"
// Include header for Epetra sparse matrix, Map (representation of
// parallel distributions), and linear problem.  Amesos uses the
// latter to encapsulate linear systems to solve.
#include "Epetra_Map.h"
#include "Epetra_CrsMatrix.h"
#include "Epetra_LinearProblem.h"
// Include header for Amesos solver.
#include "Amesos.h"
// Include header for Teuchos serial dense matrix, which we use to
// compute the eigenvectors.
#include "Teuchos_SerialDenseMatrix.hpp"
// Include header for the problem definition
#include "ModeLaplace2DQ2.h"
 
// Include selected communicator class required by Epetra objects
#ifdef EPETRA_MPI
#  include "Epetra_MpiComm.h"
#else
#  include "Epetra_SerialComm.h"
#endif
 
// \class AmesosGenOp
// \brief Operator that computes \f$Y = K^{-1} M X\f$ or \f$Y = M
//   K^{-T} X\f$, where solves with the Epetra_CrsMatrix K use an
//   Amesos solver, and M is an Epetra_Operator.
// \author Heidi K. Thornquist
// \date Jan 9, 2006
//
// This operator calls an inverse method in Apply().  It may use a
// Belos solve, Amesos solve, or AztecOO solve.  This is used to
// implement shift and invert, with a shift to zero.  Shift before you
// invert (i.e., solve).  This operator goes into Block Krylov-Schur.
//
// Anasazi will ask for the largest eigenvalues of the inverse, thus,
// the smallest eigenvalues of the original (shifted) matrix.  If you
// wanted a shift, just apply the shift first, and send that to this
// operator.
class AmesosGenOp : public virtual Epetra_Operator {
public:
  // \brief Constructor
  //
  // \param solver [in] The Amesos solver to use for solving linear
  //   systems with K.  It must already have its Epetra_LinearProblem
  //   set, and that Epetra_LinearProblem must have K.
  // \param massMtx [in] The "mass matrix" M.
  // \param useTranspose [in] If false, apply \f$K^{-1} M\f$; else,
  //   apply \f$M K^{-T}\f$.
  AmesosGenOp (const Teuchos::RCP<Amesos_BaseSolver>& solver,
               const Teuchos::RCP<Epetra_Operator>& massMtx,
               const bool useTranspose = false );
  // Destructor
  virtual ~AmesosGenOp () {}
 
  // \brief Compute Y such that \f$K^{-1} M X = Y\f$ or \f$M K^{-T} X
  //   = Y\f$, where solves with the Epetra_CrsMatrix K use an Amesos
  //   solver.
  int Apply (const Epetra_MultiVector& X, Epetra_MultiVector& Y) const;
 
  // The Operator's (human-readable) label.
  const char* Label() const {
    return "Operator that applies K^{-1} M or M K^{-T}";
  }
 
  // Whether to apply \f$K^{-1} M\f$ (false) or \f$K^{-T} M\f$ (true).
  bool UseTranspose() const { return useTranspose_; };
 
  // \brief Set whether to apply \f$K^{-1} M\f$ (false) or
  //   \f$K^{-T} M\f$ (true).
  //
  // \param useTranspose [in] If true, tell this Operator to apply
  //   \f$K^{-T} M\f$, from now until the next call to
  //   SetUseTranspose().  If false, tell this Operator to apply
  //   \f$K^{-1} M\f$, until the next call to SetUseTranspose().
  int SetUseTranspose (bool useTranspose);
 
  // The Operator's communicator.
  const Epetra_Comm& Comm () const {
    return solver_->Comm ();
  }
 
  // The Operator's domain Map.
  const Epetra_Map& OperatorDomainMap () const {
    return massMtx_->OperatorDomainMap ();
  }
 
  // The Operator's range Map.
  const Epetra_Map& OperatorRangeMap () const {
    return massMtx_->OperatorRangeMap ();
  }
 
  // \brief NOT IMPLEMENTED: Apply \f$( K^{-1} M )^{-1}\f$ or
  //   \f$( K^{-1} M )^{-T}\f$.
  //
  // Returning a nonzero value means that this Operator doesn't know
  // how to apply its inverse.
  int ApplyInverse (const Epetra_MultiVector& X, Epetra_MultiVector& Y) const {
    return -1;
  };
 
  // NOT IMPLEMENTED: Whether this Operator can compute its infinity norm.
  bool HasNormInf() const { return false; }
 
  // \brief NOT IMPLEMENTED: Infinity norm of \f$( K^{-1} M )^{-1}\f$
  //   or \f$( K^{-1} M )^{-T}\f$.
  //
  // Returning -1.0 means that the Operator does not know how to
  // compute its infinity norm.
  double NormInf () const { return -1.0; }
 
private:
  // Default constructor: You may not call this.
  AmesosGenOp () {};
 
  // Copy constructor: You may not call this.
  AmesosGenOp (const AmesosGenOp& genOp);
 
  Teuchos::RCP<Amesos_BaseSolver> solver_;
  Teuchos::RCP<Epetra_Operator> massMtx_;
  Epetra_LinearProblem* problem_;
  bool useTranspose_;
};
 
// ****************************************************************************
// BEGIN MAIN ROUTINE
// ****************************************************************************
 
int
main (int argc, char *argv[])
{
  using Teuchos::RCP;
  using Teuchos::rcp;
  using std::cerr;
  using std::cout;
  using std::endl;
  // Anasazi solvers have the following template parameters:
  //
  //   - Scalar: The type of dot product results.
  //   - MV: The type of (multi)vectors.
  //   - OP: The type of operators (functions from multivector to
  //     multivector).  A matrix (like Epetra_CrsMatrix) is an example
  //     of an operator; an Ifpack preconditioner is another example.
  //
  // Here, Scalar is double, MV is Epetra_MultiVector, and OP is
  // Epetra_Operator.
  typedef Epetra_MultiVector MV;
  typedef Epetra_Operator OP;
  typedef Anasazi::MultiVecTraits<double, MV> MVT;
 
#ifdef EPETRA_MPI
  // Initialize MPI
  MPI_Init (&argc, &argv);
  Epetra_MpiComm Comm (MPI_COMM_WORLD);
#else
  Epetra_SerialComm Comm;
#endif // EPETRA_MPI
 
  const int MyPID = Comm.MyPID ();
 
  //
  // Set up the test problem
  //
 
  // Dimensionality of the spatial domain to discretize
  const int space_dim = 2;
 
  // Size of each of the dimensions of the (discrete) domain
  std::vector<double> brick_dim (space_dim);
  brick_dim[0] = 1.0;
  brick_dim[1] = 1.0;
 
  // Number of elements in each of the dimensions of the domain
  std::vector<int> elements (space_dim);
  elements[0] = 10;
  elements[1] = 10;
 
  // Create the test problem.
  RCP<ModalProblem> testCase =
    rcp (new ModeLaplace2DQ2 (Comm, brick_dim[0], elements[0],
                              brick_dim[1], elements[1]));
 
  // Get the stiffness and mass matrices.
  //
  // rcp (T*, false) returns a nonowning (doesn't deallocate) RCP.
  RCP<Epetra_CrsMatrix> K =
    rcp (const_cast<Epetra_CrsMatrix* > (testCase->getStiffness ()), false);
  RCP<Epetra_CrsMatrix> M =
    rcp (const_cast<Epetra_CrsMatrix* > (testCase->getMass ()), false);
 
  //
  // Create linear solver for linear systems with K
  //
  // Anasazi uses shift and invert, with a "shift" of zero, to find
  // the eigenvalues of least magnitude.  In this example, we
  // implement the "invert" part of shift and invert by using an
  // Amesos direct solver.
  //
 
  // Create Epetra linear problem class for solving linear systems
  // with K.  This implements the inverse operator for shift and
  // invert.
  Epetra_LinearProblem AmesosProblem;
  // Tell the linear problem about the matrix K.  Epetra_LinearProblem
  // doesn't know about RCP, so we have to give it a raw pointer.
  AmesosProblem.SetOperator (K.get ());
 
  // Create Amesos factory and solver for solving linear systems with
  // K.  The solver uses the KLU library to do a sparse LU
  // factorization.
  //
  // Note that the AmesosProblem object "absorbs" K.  Anasazi doesn't
  // see K, just the operator that implements K^{-1} M.
  Amesos amesosFactory;
  RCP<Amesos_BaseSolver> AmesosSolver;
 
  // Amesos can interface to many different solvers.  The following
  // loop picks a solver that Amesos supports.  The loop order
  // reflects solver preference, only in the sense that using LAPACK
  // here is a suboptimal fall-back.  (With the LAPACK option, Amesos
  // makes a dense version of the sparse matrix and uses LAPACK to
  // compute the factorization.  The other options are true sparse
  // direct factorizations.)
  const int numSolverNames = 9;
  const char* solverNames[9] = {
    "Klu", "Umfpack", "Superlu", "Superludist", "Mumps",
    "Paradiso", "Taucs", "CSparse", "Lapack"
  };
  for (int k = 0; k < numSolverNames; ++k) {
    const char* const solverName = solverNames[k];
    if (amesosFactory.Query (solverName)) {
      AmesosSolver = rcp (amesosFactory.Create (solverName, AmesosProblem));
      if (MyPID == 0) {
        cout << "Amesos solver: \"" << solverName << "\"" << endl;
      }
    }
  }
  if (AmesosSolver.is_null ()) {
    throw std::runtime_error ("Amesos appears not to have any solvers enabled.");
  }
 
  // The AmesosGenOp class assumes that the symbolic and numeric
  // factorizations have already been performed on the linear problem.
  AmesosSolver->SymbolicFactorization ();
  AmesosSolver->NumericFactorization ();
 
  //
  // Set parameters for the block Krylov-Schur eigensolver
  //
 
  double tol = 1.0e-8; // convergence tolerance
  int nev = 10; // number of eigenvalues for which to solve
  int blockSize = 3; // block size (number of eigenvectors processed at once)
  int numBlocks = 3 * nev / blockSize; // restart length
  int maxRestarts = 5; // maximum number of restart cycles
 
  // We're looking for the largest-magnitude eigenvalues of the
  // _inverse_ operator, thus, the smallest-magnitude eigenvalues of
  // the original operator.
  std::string which = "LM";
  int verbosity = Anasazi::Errors + Anasazi::Warnings + Anasazi::FinalSummary;
 
  // Create ParameterList to pass into eigensolver
  Teuchos::ParameterList MyPL;
  MyPL.set ("Verbosity", verbosity);
  MyPL.set ("Which", which);
  MyPL.set ("Block Size", blockSize);
  MyPL.set ("Num Blocks", numBlocks);
  MyPL.set ("Maximum Restarts", maxRestarts);
  MyPL.set ("Convergence Tolerance", tol);
 
  // Create an initial set of vectors to start the eigensolver.  Note:
  // This needs to have the same number of columns as the block size.
  RCP<MV> ivec = rcp (new MV (K->Map (), blockSize));
  ivec->Random ();
 
  // Create the Epetra_Operator for the spectral transformation using
  // the Amesos direct solver.
  //
  // The AmesosGenOp object is the operator we give to Anasazi.  Thus,
  // Anasazi just sees an operator that computes y = K^{-1} M x.  The
  // matrix K got absorbed into AmesosProblem (the
  // Epetra_LinearProblem object).  Later, when we set up the Anasazi
  // eigensolver, we will need to tell it about M, so that it can
  // orthogonalize basis vectors with respect to the inner product
  // defined by M (since it is symmetric positive definite).
  RCP<AmesosGenOp> Aop = rcp (new AmesosGenOp (AmesosSolver, M));
 
  // Create the eigenproblem.  This object holds all the stuff about
  // your problem that Anasazi will see.
  //
  // Anasazi only needs M so that it can orthogonalize basis vectors
  // with respect to the M inner product.  Wouldn't it be nice if
  // Anasazi didn't require M in two different places?  Alas, this is
  // not currently the case.
  RCP<Anasazi::BasicEigenproblem<double,MV,OP> > MyProblem =
    rcp (new Anasazi::BasicEigenproblem<double,MV,OP> (Aop, M, ivec));
 
  // Tell the eigenproblem that the matrix pencil (K,M) is symmetric.
  MyProblem->setHermitian (true);
 
  // Set the number of eigenvalues requested
  MyProblem->setNEV (nev);
 
  // Tell the eigenproblem that you are finished passing it information.
  const bool boolret = MyProblem->setProblem ();
  if (boolret != true) {
    if (MyPID == 0) {
      cerr << "Anasazi::BasicEigenproblem::setProblem() returned with error." << endl;
    }
#ifdef EPETRA_MPI
    MPI_Finalize ();
#endif // EPETRA_MPI
    return -1;
  }
 
  // Create the Block Krylov-Schur eigensolver.
  Anasazi::BlockKrylovSchurSolMgr<double, MV, OP> MySolverMgr (MyProblem, MyPL);
 
  // Solve the eigenvalue problem.
  //
  // Note that creating the eigensolver is separate from solving it.
  // After creating the eigensolver, you may call solve() multiple
  // times with different parameters or initial vectors.  This lets
  // you reuse intermediate state, like allocated basis vectors.
  Anasazi::ReturnType returnCode = MySolverMgr.solve ();
  if (returnCode != Anasazi::Converged && MyPID == 0) {
    cout << "Anasazi eigensolver did not converge." << endl;
  }
 
  // Get the eigenvalues and eigenvectors from the eigenproblem.
  Anasazi::Eigensolution<double,MV> sol = MyProblem->getSolution ();
  // Anasazi returns eigenvalues as Anasazi::Value, so that if
  // Anasazi's Scalar type is real-valued (as it is in this case), but
  // some eigenvalues are complex, you can still access the
  // eigenvalues correctly.  In this case, there are no complex
  // eigenvalues, since the matrix pencil is symmetric.
  std::vector<Anasazi::Value<double> > evals = sol.Evals;
  RCP<MV> evecs = sol.Evecs;
  int numev = sol.numVecs;
 
  if (numev > 0) {
    // Reconstruct the eigenvalues.  The ones that Anasazi gave back
    // are the inverses of the original eigenvalues.  Reconstruct the
    // eigenvectors too.
    MV tempvec (K->Map (), MVT::GetNumberVecs (*evecs));
    K->Apply (*evecs, tempvec);
    Teuchos::SerialDenseMatrix<int,double> dmatr (numev, numev);
    MVT::MvTransMv (1.0, tempvec, *evecs, dmatr);
 
    if (MyPID == 0) {
      double compeval = 0.0;
      cout.setf (std::ios_base::right, std::ios_base::adjustfield);
      cout << "Actual Eigenvalues (obtained by Rayleigh quotient) : " << endl;
      cout << "------------------------------------------------------" << endl;
      cout << std::setw(16) << "Real Part"
           << std::setw(16) << "Rayleigh Error" << endl;
      cout << "------------------------------------------------------" << endl;
      for (int i = 0; i < numev; ++i) {
        compeval = dmatr(i,i);
        cout << std::setw(16) << compeval
             << std::setw(16)
             << std::fabs (compeval - 1.0/evals[i].realpart)
             << endl;
      }
      cout << "------------------------------------------------------" << endl;
    }
  }
 
#ifdef EPETRA_MPI
  MPI_Finalize ();
#endif // EPETRA_MPI
 
  return 0;
}
 
 
AmesosGenOp::
AmesosGenOp (const Teuchos::RCP<Amesos_BaseSolver>& solver,
             const Teuchos::RCP<Epetra_Operator>& massMtx,
             const bool useTranspose)
  : solver_ (solver),
    massMtx_ (massMtx),
    problem_ (NULL),
    useTranspose_ (useTranspose)
{
  if (solver.is_null ()) {
    throw std::invalid_argument ("AmesosGenOp constructor: The 'solver' "
                                 "input argument is null.");
  }
  if (massMtx.is_null ()) {
    throw std::invalid_argument ("AmesosGenOp constructor: The 'massMtx' "
                                 "input argument is null.");
  }
 
  Epetra_LinearProblem* problem = const_cast<Epetra_LinearProblem*> (solver->GetProblem ());
  if (problem == NULL) {
    throw std::invalid_argument ("The solver's GetProblem() method returned "
                                 "NULL.  This probably means that its "
                                 "LinearProblem has not yet been set.");
  }
  problem_ = problem;
 
  if (solver_->UseTranspose ()) {
    solver_->SetUseTranspose (! useTranspose);
  } else {
    solver_->SetUseTranspose (useTranspose);
  }
 
  if (massMtx_->UseTranspose ()) {
    massMtx_->SetUseTranspose (! useTranspose);
  } else {
    massMtx_->SetUseTranspose (useTranspose);
  }
}
 
int
AmesosGenOp::SetUseTranspose (bool useTranspose)
{
  int err = 0;
 
  if (problem_ == NULL) {
    throw std::logic_error ("AmesosGenOp::SetUseTranspose: problem_ is NULL");
  }
  if (massMtx_.is_null ()) {
    throw std::logic_error ("AmesosGenOp::SetUseTranspose: massMtx_ is null");
  }
  if (solver_.is_null ()) {
    throw std::logic_error ("AmesosGenOp::SetUseTranspose: solver_ is null");
  }
 
  const bool solverUsesTranspose = solver_->UseTranspose ();
  if (solverUsesTranspose) {
    err = solver_->SetUseTranspose (! useTranspose);
  } else {
    err = solver_->SetUseTranspose (useTranspose);
  }
 
  // If SetUseTranspose returned zero above, then the Amesos solver
  // doesn't know how to change the transpose state.
  if (err != 0) {
    return err;
  }
 
  if (massMtx_->UseTranspose ()) {
    err = massMtx_->SetUseTranspose (! useTranspose);
  } else {
    err = massMtx_->SetUseTranspose (useTranspose);
  }
 
  // If SetUseTranspose returned zero above, then the mass matrix
  // doesn't know how to change the transpose state.
  if (err != 0) {
    // Put the solver back like we found it.
    (void) solver_->SetUseTranspose (solverUsesTranspose);
    return err;
  }
 
  useTranspose_ = useTranspose;
  return 0; // the method completed correctly
}
 
int
AmesosGenOp::Apply (const Epetra_MultiVector& X, Epetra_MultiVector& Y) const
{
  if (problem_ == NULL) {
    throw std::logic_error ("AmesosGenOp::Apply: problem_ is NULL");
  }
  if (massMtx_.is_null ()) {
    throw std::logic_error ("AmesosGenOp::Apply: massMtx_ is null");
  }
  if (solver_.is_null ()) {
    throw std::logic_error ("AmesosGenOp::Apply: solver_ is null");
  }
 
  if (! useTranspose_) {
    // Storage for M*X
    Epetra_MultiVector MX (X.Map (), X.NumVectors ());
 
    // Apply M*X
    massMtx_->Apply (X, MX);
    Y.PutScalar (0.0);
 
    // Set the LHS and RHS
    problem_->SetRHS (&MX);
    problem_->SetLHS (&Y);
 
    // Solve the linear system A*Y = MX
    solver_->Solve ();
  }
  else { // apply the transposed operator
    // Storage for A^{-T}*X
    Epetra_MultiVector ATX (X.Map (), X.NumVectors ());
    Epetra_MultiVector tmpX = const_cast<Epetra_MultiVector&> (X);
 
    // Set the LHS and RHS
    problem_->SetRHS (&tmpX);
    problem_->SetLHS (&ATX);
 
    // Solve the linear system A^T*Y = X
    solver_->Solve ();
 
    // Apply M*ATX
    massMtx_->Apply (ATX, Y);
  }
 
  return 0; // the method completed correctly
}